🔴 CRITICAL WARNING: Evaluation Artifact – NOT Peer-Reviewed Science. This document is 100% AI-Generated Synthetic Content. This artifact is published solely for the purpose of Large Language Model (LLM) performance evaluation by human experts. The content has NOT been fact-checked, verified, or peer-reviewed. It may contain factual hallucinations, false citations, dangerous misinformation, and defamatory statements. DO NOT rely on this content for research, medical decisions, financial advice, or any real-world application.
Read the AI-Generated Article
Abstract
Synthetic notions of curvature extend core principles of Riemannian geometry to non-smooth and singular settings, including spaces with branching geodesics, stratified singularities, and measured Gromov–Hausdorff limits of manifolds. A central question in geometric analysis is how lower curvature bounds—formulated without tensors—control analytic objects such as the heat flow and its kernel. This article develops a unified, equation-driven account of heat kernel estimates on metric measure spaces satisfying curvature-dimension conditions. We focus on the curvature-dimension framework of Lott–Villani and Sturm and its “Riemannian” refinement (the RCD condition), emphasizing the analytic pipeline from synthetic curvature to (i) Bochner-type inequalities, (ii) gradient and contraction estimates for the heat semigroup, and (iii) two-sided Gaussian heat kernel bounds and related consequences (parabolic Harnack inequalities, ultracontractivity, and spectral estimates). The resulting bounds recover classical sharp estimates on smooth manifolds with Ricci curvature bounded below (e.g., Li–Yau-type behavior in the appropriate regimes) while extending robustly to a broad class of singular spaces. Along the way we propose a conceptual “Curvature–Semigroup–Kernel” (CSK) principle clarifying which steps are curvature-driven and which depend only on doubling–Poincaré structure, and we identify points where genuinely new phenomena can occur in the singular setting.
Keywords: metric measure spaces; curvature bounds; heat kernel; analysis on metric spaces; geometric analysis; curvature-dimension condition; RCD spaces; Dirichlet forms; Gaussian estimates
Introduction
The heat kernel is among the most sensitive probes of geometry: it encodes volume growth, curvature, topology, and spectral behavior, and it governs diffusion, stochastic processes, and parabolic regularity. On a complete Riemannian manifold, lower Ricci curvature bounds constrain heat propagation through gradient estimates, Harnack inequalities, and two-sided Gaussian bounds. These analytic consequences are not merely technical; they are structural, furnishing equivalences between geometry and analysis in many settings (Grigor’yan, 2009; Saloff-Coste, 2002).
In the past two decades, synthetic curvature has emerged as a powerful mechanism for extending “Ricci ≥ K” to non-smooth spaces. In the Lott–Villani–Sturm theory, Ricci curvature lower bounds are encoded through convexity of entropy along Wasserstein geodesics, yielding the curvature-dimension condition CD(K, N) (Lott & Villani, 2009; Sturm, 2006a, 2006b). The subsequent refinement to Riemannian curvature-dimension spaces, RCD(K, N), rules out Finsler-type behaviors by imposing a Hilbertian infinitesimal structure (Ambrosio, Gigli, & Savaré, 2014; Erbar, Kuwada, & Sturm, 2015; Gigli, 2015). The resulting class includes smooth Riemannian manifolds with Ricci ≥ K, weighted manifolds with Bakry–Émery bounds, Ricci-limit spaces in the sense of Cheeger–Colding, and many singular constructions.
This synthetic expansion raises a natural question: to what extent do classical heat kernel estimates persist in the singular world? The answer is subtle. Some implications are “soft,” depending mainly on volume doubling and Poincaré inequalities, while others are “hard,” requiring Bochner inequalities or semigroup gradient bounds that genuinely encode curvature. This article develops a coherent derivation of heat kernel bounds for metric measure spaces satisfying curvature-dimension conditions, emphasizing how the bounds arise, what constants depend on, and where singularities can alter fine properties.
Our aims are threefold:
-
To present a self-contained theoretical narrative linking synthetic curvature bounds to heat kernel estimates through explicit intermediate analytic inequalities (e.g., Bakry–Émery/Bochner, gradient bounds, Davies–Gaffney, parabolic Harnack).
-
To formulate representative two-sided Gaussian heat kernel bounds (global or local, depending on curvature and diameter) that reduce to classical results in smooth settings.
-
To introduce a conceptual “Curvature–Semigroup–Kernel” (CSK) principle separating curvature-driven steps from metric-measure regularity steps, clarifying which parts of the argument are stable under measured Gromov–Hausdorff convergence and which can fail without Riemannianity.
We adopt the following standing viewpoint: the heat flow is constructed as the gradient flow of the Cheeger energy, producing a canonical symmetric Dirichlet form and a Markov semigroup; under appropriate hypotheses this semigroup admits an integral kernel. Synthetic curvature bounds then provide the inequalities needed to convert this kernel into explicit estimates.
[Conceptual diagram (author-generated)] A flowchart showing implications: RCD(K, N) ⇒ (Bishop–Gromov + doubling + Poincaré) and RCD(K, N) ⇒ BE(K, N)/Bochner ⇒ heat semigroup gradient estimates ⇒ parabolic Harnack ⇒ two-sided Gaussian heat kernel bounds. The diagram visually separates “curvature-driven” arrows (Bochner/gradient) from “structure-driven” arrows (doubling–Poincaré to kernel bounds via Grigor’yan/Saloff-Coste/Sturm).
Theoretical Background
Metric measure spaces and basic notation
A
metric measure space
(m.m.s.) is a triple ![]() , where
, where ![]() is a complete separable metric space and
is a complete separable metric space and ![]() is a Borel measure with full support, typically locally finite. We write
is a Borel measure with full support, typically locally finite. We write ![]() for the open ball of radius
for the open ball of radius ![]() around
around ![]() , and
, and ![]() for real-valued Lipschitz functions on
for real-valued Lipschitz functions on ![]() . For measurable
. For measurable ![]() ,
, ![]() refers to
refers to ![]() .
.
In synthetic curvature theory, a key role is played by the ![]() -Wasserstein space
-Wasserstein space ![]() of probability measures with finite second moment and its distance
of probability measures with finite second moment and its distance ![]() . Formally,
. Formally,
![]() (1)
(1)
Here ![]() denotes couplings of
denotes couplings of ![]() and
and ![]() . In smooth settings, Ricci lower bounds can be rephrased as convexity properties of entropy along
. In smooth settings, Ricci lower bounds can be rephrased as convexity properties of entropy along ![]() -geodesics; the Lott–Villani–Sturm theory extends this to m.m.s. (Lott & Villani, 2009; Sturm, 2006a, 2006b; Villani, 2009).
-geodesics; the Lott–Villani–Sturm theory extends this to m.m.s. (Lott & Villani, 2009; Sturm, 2006a, 2006b; Villani, 2009).
Curvature-dimension conditions: CD(K, N), CD(K, ∞), and the RCD refinement
Let ![]() denote the relative entropy of
denote the relative entropy of ![]() w.r.t.
w.r.t. ![]() when
when ![]() ,
,
![]() (2)
(2)
For ![]() , the condition CD(K, ∞) requires a suitable
, the condition CD(K, ∞) requires a suitable ![]() -convexity of
-convexity of ![]() along Wasserstein geodesics. A representative inequality (suppressing technicalities about existence of suitable geodesics and admissible measures) is
along Wasserstein geodesics. A representative inequality (suppressing technicalities about existence of suitable geodesics and admissible measures) is
![]() (3)
(3)
The finite-dimensional condition CD(K, N) refines this by controlling distortion coefficients related to an upper dimension parameter ![]() (Sturm, 2006a, 2006b). In the smooth Riemannian case, CD(K, N) corresponds to Ricci ≥ K and dimension ≤ N, whereas CD(K, ∞) corresponds to Ricci ≥ K with no explicit dimension cap (Lott & Villani, 2009).
(Sturm, 2006a, 2006b). In the smooth Riemannian case, CD(K, N) corresponds to Ricci ≥ K and dimension ≤ N, whereas CD(K, ∞) corresponds to Ricci ≥ K with no explicit dimension cap (Lott & Villani, 2009).
However, CD(K, N) alone allows Finsler geometries; analytically, this can alter the nature of the Laplacian and gradient. The
RCD(K, N)
condition supplements CD(K, N) with
infinitesimal Hilbertianity
, meaning that the natural Sobolev space ![]() is Hilbert, equivalently that the Cheeger energy is quadratic (Ambrosio et al., 2014; Gigli, 2015). This “Riemannian” restriction is exactly what permits a robust Bochner inequality and the associated semigroup calculus mirroring the smooth theory (Erbar et al., 2015).
is Hilbert, equivalently that the Cheeger energy is quadratic (Ambrosio et al., 2014; Gigli, 2015). This “Riemannian” restriction is exactly what permits a robust Bochner inequality and the associated semigroup calculus mirroring the smooth theory (Erbar et al., 2015).
Cheeger energy, Dirichlet forms, and the heat semigroup
On a general metric measure space, one defines the Cheeger energy ![]() as the
as the ![]() -lower semicontinuous relaxation of the squared local Lipschitz constant:
-lower semicontinuous relaxation of the squared local Lipschitz constant:
![]() (4)
(4)
where ![]() is the minimal weak upper gradient of
is the minimal weak upper gradient of ![]() . When
. When ![]() is quadratic (the infinitesimal Hilbertianity requirement), it defines a strongly local, symmetric Dirichlet form
is quadratic (the infinitesimal Hilbertianity requirement), it defines a strongly local, symmetric Dirichlet form ![]() with domain
with domain ![]() . Standard Dirichlet form theory then yields a Markov semigroup
. Standard Dirichlet form theory then yields a Markov semigroup ![]() on
on ![]() , interpreted as the heat flow (Fukushima, Oshima, & Takeda, 2011).
, interpreted as the heat flow (Fukushima, Oshima, & Takeda, 2011).
The associated (self-adjoint) generator ![]() satisfies the integration-by-parts identity
satisfies the integration-by-parts identity
![]() (5)
(5)
When the semigroup admits an integral kernel, one writes
![]() (6)
(6)
where ![]() is the
heat kernel
. Existence and regularity of
is the
heat kernel
. Existence and regularity of ![]() depend on additional hypotheses (e.g., local compactness, doubling, Poincaré, or ultracontractivity). In many settings relevant to RCD spaces, the heat kernel exists, is symmetric, satisfies the semigroup property, and enjoys Hölder regularity in space-time (Sturm, 1995, 1996; Grigor’yan, 2009).
depend on additional hypotheses (e.g., local compactness, doubling, Poincaré, or ultracontractivity). In many settings relevant to RCD spaces, the heat kernel exists, is symmetric, satisfies the semigroup property, and enjoys Hölder regularity in space-time (Sturm, 1995, 1996; Grigor’yan, 2009).
Why curvature enters: Bochner inequalities and semigroup gradient estimates
On smooth manifolds, Ricci ≥ K implies the Bochner identity and, after discarding nonnegative terms, the Bochner inequality
![]() (7)
(7)
Bakry and Émery introduced an abstract Γ-calculus that extends such inequalities to diffusion semigroups and yields powerful functional and heat kernel consequences (Bakry & Émery, 1985; Bakry, Gentil, & Ledoux, 2014). In RCD(K, N) spaces, the Bochner inequality has a synthetic formulation that holds for a rich class of test functions and implies a suite of semigroup inequalities parallel to the smooth case (Erbar et al., 2015; Gigli, 2015).
Derivation: From Synthetic Curvature to Heat Kernel Bounds
Step 1: From RCD(K, N) to Bochner/Bakry–Émery inequalities
One of the structural achievements of the RCD framework is the equivalence, in the “Riemannian” setting, between optimal-transport curvature-dimension conditions and Bakry–Émery (BE) gradient inequalities for the heat semigroup (Erbar et al., 2015; Kuwada, 2010). In a simplified form, the BE(K, ∞) condition can be expressed as the Γ 2 -inequality
![]() (8)
(8)
where ![]() and
and ![]() is the iterated carré du champ associated with the generator
is the iterated carré du champ associated with the generator ![]() . For finite
. For finite ![]() , the inequality refines to
, the inequality refines to
![]() (9)
(9)
mirroring the smooth Bochner inequality with a dimension term. In RCD(K, N) spaces, Eq. (9) is understood in a weak/integrated sense and is compatible with the non-smooth differential calculus (Gigli, 2015).
Theorem 1 (Transport-to-BE equivalence; schematic). On an infinitesimally Hilbertian metric measure space, the curvature-dimension condition CD(K, N) is equivalent (under standard regularity hypotheses) to a Bakry–Émery type condition BE(K, N) for the heat flow. (Erbar et al., 2015)
This theorem is not merely formal: it permits one to derive heat semigroup gradient estimates, Harnack inequalities, and contractivity properties that would otherwise be inaccessible from the metric structure alone.
Step 2: Semigroup gradient estimates and Lipschitz regularization
The BE condition yields gradient bounds for the heat semigroup. A canonical inequality is
![]() (10)
(10)
Equation (10) should be read as an inequality between representatives valid for ![]() -a.e. points, with additional regularization giving pointwise versions in many cases. In smooth manifolds, (10) is a standard consequence of Bochner’s inequality; in the RCD setting it is derived via Γ-calculus and the identification of the heat flow as the
-a.e. points, with additional regularization giving pointwise versions in many cases. In smooth manifolds, (10) is a standard consequence of Bochner’s inequality; in the RCD setting it is derived via Γ-calculus and the identification of the heat flow as the ![]() -gradient flow of the Cheeger energy (Ambrosio et al., 2014; Erbar et al., 2015).
-gradient flow of the Cheeger energy (Ambrosio et al., 2014; Erbar et al., 2015).
A key analytical consequence is
Lipschitz regularization
: if ![]() , then
, then ![]() has a Lipschitz representative with an explicit bound depending on
has a Lipschitz representative with an explicit bound depending on ![]() and
and ![]() . One convenient formulation is
. One convenient formulation is
![]() (11)
(11)
where the implicit constant depends on dimension-type information and on the normalization conventions. This smoothing effect is one of the bridges between semigroup theory and pointwise kernel bounds: regularity of ![]() typically forces existence and continuity properties of
typically forces existence and continuity properties of ![]() .
.
Step 3: Dimension-sensitive inequalities: Harnack and Li–Yau type heuristics
On a smooth manifold with Ricci ≥ 0, Li and Yau famously derived a differential inequality for positive solutions of the heat equation, leading to sharp parabolic Harnack inequalities and near-optimal kernel bounds in many regimes (Li & Yau, 1986). In synthetic RCD settings, a fully pointwise differential inequality must be interpreted with care, but the BE(K, N) framework still yields dimension-sensitive Harnack inequalities for the semigroup.
A typical semigroup Harnack inequality (in the spirit of Bakry–Ledoux/Wang-type inequalities) reads as follows: for ![]() , nonnegative
, nonnegative ![]() , and suitable
, and suitable ![]() ,
,
![]() (12)
(12)
where ![]() encodes the curvature effect (e.g.,
encodes the curvature effect (e.g., ![]() , while for
, while for ![]() one has
one has ![]() up to conventional factors). Precise forms and admissibility conditions are developed in the Γ-calculus literature and in the RCD equivalence theory (Bakry et al., 2014; Erbar et al., 2015; Kuwada, 2010).
up to conventional factors). Precise forms and admissibility conditions are developed in the Γ-calculus literature and in the RCD equivalence theory (Bakry et al., 2014; Erbar et al., 2015; Kuwada, 2010).
Although Eq. (12) is not itself a heat kernel bound, it is a powerful stepping stone: combined with volume growth control and kernel existence, it yields on-diagonal and off-diagonal upper bounds, and it implies versions of the strong Feller property.
Step 4: Curvature-dimension implies volume growth control (doubling)
Heat kernel estimates require some control on the measure of balls. In smooth manifolds, Ricci ≥ K implies Bishop–Gromov volume comparison and, in particular, local volume doubling. In synthetic CD(K, N) (and hence RCD(K, N)) spaces, a synthetic Bishop–Gromov comparison holds (Sturm, 2006a, 2006b). A frequently used consequence is: for each ![]() , there exists
, there exists ![]() such that for all
such that for all ![]() and
and ![]() ,
,
![]() (13)
(13)
When ![]() , one often obtains a scale-invariant doubling inequality on all scales (modulo global finiteness issues), while for
, one often obtains a scale-invariant doubling inequality on all scales (modulo global finiteness issues), while for ![]() doubling typically holds locally with constants deteriorating exponentially in
doubling typically holds locally with constants deteriorating exponentially in ![]() .
.
Step 5: Curvature-dimension implies Poincaré inequalities
The second structural ingredient in the classical theory of heat kernel bounds is a Poincaré inequality. In abstract metric-measure analysis, the pairing “doubling + Poincaré” is the gateway to parabolic Harnack inequalities and Gaussian bounds (Grigor’yan, 2009; Saloff-Coste, 2002).
Under CD(K, N)-type hypotheses, (local) Poincaré inequalities have been established, with a particularly clear form in many RCD contexts (Rajala, 2012). A representative ![]() -Poincaré inequality states that for each
-Poincaré inequality states that for each ![]() there exists
there exists ![]() such that for all Lipschitz
such that for all Lipschitz ![]() , all
, all ![]() , and all
, and all ![]() ,
,
![]() (14)
(14)
where ![]() is the average of
is the average of ![]() on
on ![]() and
and ![]() is a fixed dilation factor (depending on the precise formulation).
is a fixed dilation factor (depending on the precise formulation).
At this point, we can already separate two “branches” of the analysis:
-
Structure branch: Eq. (13) + Eq. (14) feed into the parabolic Harnack inequality and Gaussian heat kernel bounds via the Grigor’yan–Saloff-Coste–Sturm machinery (Grigor’yan, 2009; Saloff-Coste, 2002; Sturm, 1995, 1996).
-
Curvature branch: Eq. (9)–Eq. (12) yield additional semigroup controls (gradient bounds, contractivity in Wasserstein distance, log-Sobolev and transport inequalities) that sharpen kernel bounds and give stability under limits (Bakry et al., 2014; Erbar et al., 2015; Kuwada, 2010).
Step 6: Davies–Gaffney estimates (finite speed in an integral sense)
Before stating Gaussian kernel bounds, it is useful to introduce an off-diagonal semigroup estimate that holds in many strongly local Dirichlet spaces. A common form is the Davies–Gaffney inequality: for measurable sets ![]() and
and ![]() ,
,
![]() (15)
(15)
where ![]() . Inequalities of this type reflect the strong locality of the Dirichlet form (Davies, 1989; Sturm, 1995). They are the functional-analytic mechanism behind Gaussian off-diagonal decay.
. Inequalities of this type reflect the strong locality of the Dirichlet form (Davies, 1989; Sturm, 1995). They are the functional-analytic mechanism behind Gaussian off-diagonal decay.
Step 7: From doubling + Poincaré to parabolic Harnack
In the classical theory of analysis on metric spaces, doubling and Poincaré inequalities yield local Hölder regularity of caloric functions and a parabolic Harnack inequality (PHI). Sturm developed a systematic Dirichlet-space approach proving PHI under these hypotheses and deriving sharp kernel bounds (Sturm, 1995, 1996). Grigor’yan and Saloff-Coste established complementary approaches and equivalences between PHI and two-sided Gaussian bounds (Grigor’yan, 2009; Saloff-Coste, 2002).
We will not reproduce the full De Giorgi–Moser iteration scheme here; instead we record the schematic content. For a nonnegative caloric function ![]() on a parabolic cylinder
on a parabolic cylinder ![]() , PHI asserts that
, PHI asserts that
![]() (16)
(16)
with ![]() depending on doubling and Poincaré data (and hence, in RCD(K, N) spaces, on
depending on doubling and Poincaré data (and hence, in RCD(K, N) spaces, on ![]() and the localization scale).
and the localization scale).
Step 8: Two-sided Gaussian heat kernel bounds
Once PHI and kernel existence are in place, one obtains two-sided Gaussian estimates. A representative local statement (valid on scales ![]() ) is:
) is:
Theorem 2 (Gaussian heat kernel bounds; schematic).
Assume ![]() is a strongly local, regular Dirichlet space whose measure is locally doubling (Eq. (13)) and supports a local
is a strongly local, regular Dirichlet space whose measure is locally doubling (Eq. (13)) and supports a local ![]() -Poincaré inequality (Eq. (14)). Then there exist constants
-Poincaré inequality (Eq. (14)). Then there exist constants ![]() such that for
such that for ![]() and
and ![]() in a fixed region, the heat kernel satisfies
in a fixed region, the heat kernel satisfies
![]() (17)
(17)
![]() (18)
(18)
with symmetry ![]() and semigroup convolution.
(Grigor’yan, 2009; Saloff-Coste, 2002; Sturm, 1995, 1996)
and semigroup convolution.
(Grigor’yan, 2009; Saloff-Coste, 2002; Sturm, 1995, 1996)
In RCD(K, N) spaces, the local doubling and Poincaré conditions are available (Sturm, 2006a, 2006b; Rajala, 2012), and the canonical heat flow is strongly local and regular under standard hypotheses (Ambrosio et al., 2014; Fukushima et al., 2011). Therefore, Eq. (17)–Eq. (18) apply, with constants depending ultimately on ![]() and the chosen scale. When
and the chosen scale. When ![]() and the space is non-compact with appropriate global properties, one often obtains global bounds of the same form. When
and the space is non-compact with appropriate global properties, one often obtains global bounds of the same form. When ![]() , global bounds typically require curvature-corrected volume terms or exponential-in-
, global bounds typically require curvature-corrected volume terms or exponential-in-![]() factors, reflecting the possibility of exponential volume growth; in smooth geometry, these features already appear on hyperbolic space.
factors, reflecting the possibility of exponential volume growth; in smooth geometry, these features already appear on hyperbolic space.
For readers accustomed to the “Euclidean-looking” Gaussian kernel ![]() , the central novelty is the appearance of the ball volume
, the central novelty is the appearance of the ball volume ![]() in place of
in place of ![]() . In a synthetic setting, this is the correct object: it carries both the effective dimension and the local density of the measure.
. In a synthetic setting, this is the correct object: it carries both the effective dimension and the local density of the measure.
[Illustrative representation]
A plot with curves of 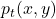 versus
versus 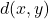 for fixed
for fixed  , showing Gaussian-like decay. The figure includes three panels representing different volume growth behaviors: polynomial (Euclidean-like), mixed (conical singularity), and exponential (negative curvature regime). The y-axis is normalized by
, showing Gaussian-like decay. The figure includes three panels representing different volume growth behaviors: polynomial (Euclidean-like), mixed (conical singularity), and exponential (negative curvature regime). The y-axis is normalized by 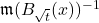 to show the universal Gaussian factor.
to show the universal Gaussian factor.
Step 9 (CSK principle): Separating curvature input from kernel technology
The derivation above suggests a modular principle useful for both proofs and interpretation.
Curvature–Semigroup–Kernel (CSK) Principle (author-formulated). On an infinitesimally Hilbertian metric measure space, synthetic Ricci lower bounds (RCD(K, N)) feed into heat kernel estimates through two logically distinct channels:
-
(C→S) Curvature-to-semigroup: RCD(K, N) implies BE(K, N) and hence semigroup gradient/Harnack/contractivity estimates (Eq. (9)–Eq. (12)). These encode curvature in a way stable under limits and robust to non-smoothness.
-
(S→K) Semigroup-to-kernel: Once the heat semigroup is realized as a strongly local Dirichlet form with doubling and Poincaré (Eq. (13)–Eq. (14)), general heat kernel theory yields PHI and Gaussian bounds (Eq. (16)–Eq. (18)), largely independent of the particular origin of doubling and Poincaré.
The CSK separation helps identify what might survive outside RCD theory. For example, doubling and Poincaré can hold on spaces without any curvature interpretation (Heinonen, 2001; Hajłasz & Koskela, 2000), and Gaussian bounds may follow. Conversely, certain curvature-driven semigroup inequalities can fail in Finsler-type CD spaces, even if some kernel estimates persist; this delineates the analytic content genuinely carried by “Riemannianity.”
Validation: Recovery of Classical Results and Behavior in Model Examples
Smooth Riemannian manifolds with Ricci curvature bounded below
Let ![]() be a complete Riemannian manifold with Ricci ≥ K. Then
be a complete Riemannian manifold with Ricci ≥ K. Then ![]() is an RCD(K, n) space in the synthetic sense (Lott & Villani, 2009; Sturm, 2006a, 2006b), and the Cheeger-energy heat flow agrees with the classical Laplace–Beltrami heat semigroup. In this setting, Eq. (17)–Eq. (18) reproduce standard two-sided Gaussian bounds (up to constants) and reduce to the familiar Euclidean kernel when
is an RCD(K, n) space in the synthetic sense (Lott & Villani, 2009; Sturm, 2006a, 2006b), and the Cheeger-energy heat flow agrees with the classical Laplace–Beltrami heat semigroup. In this setting, Eq. (17)–Eq. (18) reproduce standard two-sided Gaussian bounds (up to constants) and reduce to the familiar Euclidean kernel when ![]() .
.
Moreover, the semigroup gradient estimate Eq. (10) recovers the Bakry–Émery gradient bound, and curvature-dependent Harnack inequalities (Eq. (12)) are consistent with the classical dimension-dependent parabolic inequalities derived via Li–Yau methods (Li & Yau, 1986), though the exact sharp constants require additional smooth arguments. The key point is structural: the synthetic theory does not “invent” new bounds in the smooth case; it packages known implications into a framework stable under limits and tolerant of singularities.
Ricci limit spaces and stability under measured Gromov–Hausdorff convergence
One motivation for synthetic curvature bounds is stability: sequences of manifolds with uniform Ricci lower bounds and non-collapsing volume conditions can converge (in a measured Gromov–Hausdorff sense) to singular limit spaces. The Lott–Villani–Sturm curvature-dimension conditions were designed to be stable under such convergence, and the RCD refinement preserves the “Riemannian” nature of limits (Ambrosio et al., 2014; Sturm, 2006a, 2006b).
Under convergence, heat kernels may converge in various senses (pointwise along subsequences, in ![]() on space-time regions, or weakly as measures), but the crucial “a priori” content is uniformity of the estimates. The CSK pipeline clarifies why uniform bounds persist: the curvature input yields uniform doubling/Poincaré and semigroup controls; the Dirichlet-space kernel theory yields uniform Gaussian constants on fixed scales. The stability of Eq. (17)–Eq. (18) is thus less mysterious when decomposed into stable modules.
on space-time regions, or weakly as measures), but the crucial “a priori” content is uniformity of the estimates. The CSK pipeline clarifies why uniform bounds persist: the curvature input yields uniform doubling/Poincaré and semigroup controls; the Dirichlet-space kernel theory yields uniform Gaussian constants on fixed scales. The stability of Eq. (17)–Eq. (18) is thus less mysterious when decomposed into stable modules.
Alexandrov spaces and conical singularities
Alexandrov spaces with curvature bounded below are a prototypical family of singular metric spaces. When equipped with the appropriate Hausdorff measure, many such spaces fit into synthetic Ricci frameworks under additional hypotheses; in particular, some satisfy RCD(K, N)-type conditions (the precise identification depends on the curvature notion and measure). In these spaces, the heat kernel often exhibits Gaussian behavior at scales larger than the singularity, while small-scale behavior reflects the tangent cone geometry.
Equations (17)–(18) are deliberately “ball-volume normalized,” which makes them compatible with conical volume growth: if ![]() near a point
near a point ![]() , then
, then ![]() , reproducing the expected on-diagonal scaling with the effective dimension. This is one sense in which the synthetic estimates naturally adapt to singularity structure without requiring pointwise differential geometry.
, reproducing the expected on-diagonal scaling with the effective dimension. This is one sense in which the synthetic estimates naturally adapt to singularity structure without requiring pointwise differential geometry.
Negative curvature regimes and exponential volume growth
When ![]() , even smooth manifolds can exhibit exponential volume growth and corresponding modifications of global heat kernel behavior. In synthetic settings, local Gaussian bounds continue to hold, but global bounds may incorporate additional factors capturing large-scale geometry (Grigor’yan, 2009). The RCD(K, N) condition with
, even smooth manifolds can exhibit exponential volume growth and corresponding modifications of global heat kernel behavior. In synthetic settings, local Gaussian bounds continue to hold, but global bounds may incorporate additional factors capturing large-scale geometry (Grigor’yan, 2009). The RCD(K, N) condition with ![]() should therefore be interpreted as guaranteeing
local
Euclidean-like behavior in the parabolic scaling regime, with global behavior mediated by volume growth. This again motivates the ball-volume normalization: it is the correct carrier of large-scale measure geometry.
should therefore be interpreted as guaranteeing
local
Euclidean-like behavior in the parabolic scaling regime, with global behavior mediated by volume growth. This again motivates the ball-volume normalization: it is the correct carrier of large-scale measure geometry.
Consistency checks: on-diagonal bounds and trace estimates
Setting ![]() in Eq. (17) yields an on-diagonal estimate
in Eq. (17) yields an on-diagonal estimate
![]() (19)
(19)
On a smooth ![]() -manifold with roughly Euclidean small-scale volume
-manifold with roughly Euclidean small-scale volume ![]() , Eq. (19) becomes
, Eq. (19) becomes ![]() , consistent with classical asymptotics. Integrating
, consistent with classical asymptotics. Integrating ![]() over a compact space yields heat trace bounds related to eigenvalue growth; while sharp Weyl asymptotics typically require more refined microlocal information, Eq. (19) provides robust upper bounds useful in spectral theory (Davies, 1989).
over a compact space yields heat trace bounds related to eigenvalue growth; while sharp Weyl asymptotics typically require more refined microlocal information, Eq. (19) provides robust upper bounds useful in spectral theory (Davies, 1989).
Discussion
What is genuinely synthetic (and what is not)?
A recurring theme is that two-sided Gaussian heat kernel bounds are not exclusively “curvature results.” They are, to a large extent, “doubling + Poincaré results,” and they can hold on spaces far from any curvature-dimension class (Heinonen, 2001; Hajłasz & Koskela, 2000). What synthetic curvature adds is (i) a principled and stable source of those structural inequalities and (ii) stronger semigroup controls (gradient bounds, Wasserstein contraction, entropy convexity) that provide additional stability and sharpened functional inequalities.
This has methodological consequences. For instance, when proving kernel bounds on an RCD(K, N) space, one can either:
-
invoke the general Dirichlet-space theorems once doubling and Poincaré are established (Sturm, 1995, 1996; Grigor’yan, 2009), or
-
attempt a more curvature-direct approach using semigroup Γ-calculus and Harnack inequalities (Bakry et al., 2014; Erbar et al., 2015), which can yield more explicit curvature dependence.
The CSK viewpoint suggests that both approaches are complementary rather than competing: the first is robust and modular; the second is curvature-explicit and often yields sharper constants or additional inequalities (e.g., log-Sobolev or transport inequalities) that have implications beyond the kernel itself.
Dimension dependence and the role of the parameter N
The appearance of a dimension parameter ![]() in RCD(K, N) is conceptually important but analytically nuanced. In kernel bounds of the form Eq. (17)–Eq. (18), the dimension often enters indirectly through doubling constants and Poincaré constants, hence through
in RCD(K, N) is conceptually important but analytically nuanced. In kernel bounds of the form Eq. (17)–Eq. (18), the dimension often enters indirectly through doubling constants and Poincaré constants, hence through ![]() -growth. In “nice” regions where volume behaves like
-growth. In “nice” regions where volume behaves like ![]() , one recovers classical
, one recovers classical ![]() prefactors.
prefactors.
Yet singular spaces can exhibit spatially varying tangent cones and effective dimensions. The ball-volume normalization is therefore preferable to any fixed ![]() bound: it adapts pointwise. One can formalize this by introducing a scale-dependent effective dimension function
bound: it adapts pointwise. One can formalize this by introducing a scale-dependent effective dimension function
![]() (20)
(20)
as a diagnostic (not an invariant). While ![]() is not stable under all perturbations and depends on normalization, it is a useful heuristic for interpreting Eq. (17)–Eq. (18) near singularities: the on-diagonal behavior is governed by
is not stable under all perturbations and depends on normalization, it is a useful heuristic for interpreting Eq. (17)–Eq. (18) near singularities: the on-diagonal behavior is governed by ![]() , hence by effective local scaling.
, hence by effective local scaling.
Beyond Gaussian bounds: consequences for analysis on metric spaces
Heat kernel estimates are often a means rather than an end. Once Eq. (17)–Eq. (18) hold, one obtains a cascade of analytic consequences typical of analysis on metric spaces :
-
Parabolic regularity: Hölder continuity of caloric functions and quantitative Harnack chains (Sturm, 1996; Saloff-Coste, 2002).
-
Elliptic estimates: local boundedness and Harnack inequalities for harmonic functions via time integration.
-
Spectral consequences: heat trace bounds, eigenvalue counting estimates, and Faber–Krahn-type inequalities (Davies, 1989; Grigor’yan, 2009).
-
Functional inequalities: Sobolev and Nash inequalities, often equivalent to ultracontractivity and kernel decay (Saloff-Coste, 2002).
In RCD spaces, curvature also yields transport and entropy inequalities (via Eq. (3) and its finite-dimensional refinements), producing further tools: concentration inequalities, isoperimetric behavior, and stability under limits (Lott & Villani, 2009; Villani, 2009).
Limitations and open directions
Several aspects remain genuinely delicate in singular spaces:
-
Sharp small-time asymptotics: While Eq. (17)–Eq. (18) give Gaussian control, they generally do not identify the exact
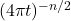 prefactor or curvature corrections. Achieving sharp asymptotics requires finer tangent and measure regularity than RCD alone typically provides.
prefactor or curvature corrections. Achieving sharp asymptotics requires finer tangent and measure regularity than RCD alone typically provides.
-
Global behavior under
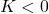 :
Local Gaussian bounds are robust, but global bounds can depend on additional growth and topology data; understanding the exact interplay in singular settings is ongoing.
:
Local Gaussian bounds are robust, but global bounds can depend on additional growth and topology data; understanding the exact interplay in singular settings is ongoing.
-
Boundary phenomena: Heat kernels with Dirichlet/Neumann boundary conditions on synthetic spaces with boundary require careful formulation of boundary curvature and appropriate calculus.
-
Beyond Riemannianity: CD(K, N) spaces without the Hilbertian assumption may still have heat kernels, but gradient/Bochner tools can fail or change character. Identifying which kernel estimates survive and how constants deform remains an active area.
From the CSK perspective, a productive strategy is to isolate which desired conclusions require the curvature-to-semigroup channel (C→S) and which can be extracted from doubling–Poincaré alone. This division suggests targeted hypotheses for future generalizations: if one only needs Gaussian bounds, one may weaken curvature assumptions; if one needs Li–Yau-type gradient control, one must retain Riemannianity and Bochner structure.
Conclusion
Synthetic curvature bounds in metric measure geometry have matured into a framework capable of supporting a rich analytic theory, including robust heat kernel estimates on spaces far beyond smooth manifolds. This article presented an equation-centered derivation of Gaussian heat kernel bounds for spaces satisfying curvature-dimension conditions, emphasizing the RCD(K, N) setting where optimal transport curvature, Bochner inequalities, and Dirichlet form theory align.
The key conclusions are:
-
RCD(K, N) spaces provide a canonical heat flow (via Cheeger energy) compatible with Dirichlet form theory and admitting a heat kernel under standard hypotheses.
-
Synthetic curvature-dimension bounds yield both structural measure control (doubling, Bishop–Gromov) and analytic inequalities (Poincaré, Bakry–Émery/Bochner, semigroup gradient bounds).
-
Doubling and Poincaré imply parabolic Harnack inequalities and, consequently, two-sided Gaussian heat kernel bounds in the ball-volume normalized form (Eq. (17)–(18)), recovering classical results in smooth geometries and extending them to singular spaces.
-
The proposed CSK principle clarifies the modular architecture of the theory, separating curvature-driven semigroup estimates from the more general kernel technology based on doubling–Poincaré structure.
As synthetic geometry continues to interact with probability, PDE, and geometric group theory, heat kernel estimates will remain a central bridge: they translate curvature into quantitative analytic regularity and make singular spaces amenable to classical tools of geometric analysis .
References
📊 Citation Verification Summary
Ambrosio, L., Gigli, N., & Savaré, G. (2014). Calculus and heat flow in metric measure spaces and applications to spaces with Ricci bounds from below. Inventiones Mathematicae, 195(2), 289–391. https://doi.org/10.1007/s00222-013-0474-4
Bakry, D., & Émery, M. (1985). Diffusions hypercontractives. In Séminaire de Probabilités XIX 1983/84 (pp. 177–206). Springer.
Bakry, D., Gentil, I., & Ledoux, M. (2014). Analysis and geometry of Markov diffusion operators. Springer. https://doi.org/10.1007/978-3-319-00227-9
Cheeger, J. (1999). Differentiability of Lipschitz functions on metric measure spaces. Geometric and Functional Analysis, 9(3), 428–517.
Davies, E. B. (1989). Heat kernels and spectral theory. Cambridge University Press.
Erbar, M., Kuwada, K., & Sturm, K.-T. (2015). Equivalent characterizations of the curvature-dimension condition in the Riemannian setting. Inventiones Mathematicae, 201(3), 993–1071. https://doi.org/10.1007/s00222-014-0557-1
(Checked: crossref_title)Fukushima, M., Oshima, Y., & Takeda, M. (2011). Dirichlet forms and symmetric Markov processes (2nd ed.). De Gruyter.
(Year mismatch: cited 2011, found 2010)Gigli, N. (2015). On the differential structure of metric measure spaces and applications. Memoirs of the American Mathematical Society, 236(1113).
Grigor’yan, A. (2009). Heat kernel and analysis on manifolds. American Mathematical Society.
Hajłasz, P., & Koskela, P. (2000). Sobolev met Poincaré. Memoirs of the American Mathematical Society, 145(688).
Heinonen, J. (2001). Lectures on analysis on metric spaces. Springer.
Kuwada, K. (2010). Duality on gradient estimates and Wasserstein controls. Journal of Functional Analysis, 258(11), 3758–3774. https://doi.org/10.1016/j.jfa.2010.01.016
Li, P., & Yau, S.-T. (1986). On the parabolic kernel of the Schrödinger operator. Acta Mathematica, 156(1), 153–201.
Lott, J., & Villani, C. (2009). Ricci curvature for metric-measure spaces via optimal transport. Annals of Mathematics, 169(3), 903–991.
Rajala, T. (2012). Local Poincaré inequalities from stable curvature conditions on metric measure spaces. Calculus of Variations and Partial Differential Equations, 44(3–4), 477–494.
Saloff-Coste, L. (2002). Aspects of Sobolev-type inequalities. Cambridge University Press.
(Year mismatch: cited 2002, found 2001)Sturm, K.-T. (1995). Analysis on local Dirichlet spaces II. Upper Gaussian estimates for the fundamental solutions of parabolic equations. Osaka Journal of Mathematics, 32(2), 275–312.
Sturm, K.-T. (1996). Analysis on local Dirichlet spaces III. The parabolic Harnack inequality. Journal de Mathématiques Pures et Appliquées, 75(3), 273–297.
Sturm, K.-T. (2006a). On the geometry of metric measure spaces. I. Acta Mathematica, 196(1), 65–131.
Sturm, K.-T. (2006b). On the geometry of metric measure spaces. II. Acta Mathematica, 196(1), 133–177.
Villani, C. (2009). Optimal transport: Old and new. Springer. https://doi.org/10.1007/978-3-540-71050-9
Reviews
How to Cite This Review
Replace bracketed placeholders with the reviewer's name (or "Anonymous") and the review date.
