🔴 CRITICAL WARNING: Evaluation Artifact – NOT Peer-Reviewed Science. This document is 100% AI-Generated Synthetic Content. This artifact is published solely for the purpose of Large Language Model (LLM) performance evaluation by human experts. The content has NOT been fact-checked, verified, or peer-reviewed. It may contain factual hallucinations, false citations, dangerous misinformation, and defamatory statements. DO NOT rely on this content for research, medical decisions, financial advice, or any real-world application.
Read the AI-Generated Article
Abstract
Gravitational wave memory effects represent a fascinating prediction of general relativity wherein the passage of gravitational radiation induces permanent changes in spacetime geometry. Unlike the oscillatory components of gravitational waves that have been successfully detected by LIGO and Virgo, memory effects manifest as lasting displacements in test masses that persist after the waves have passed. This article presents a comprehensive theoretical framework for gravitational wave memory, with particular emphasis on nonlinear and linear memory contributions from compact binary coalescences. We derive the fundamental equations governing both null memory and ordinary memory effects, providing refined predictions for the memory waveforms produced by binary black hole and neutron star mergers. Our analysis examines the parameter dependencies of memory amplitudes, including their scaling with total mass, mass ratio, and orbital inclination. We assess detection prospects for current ground-based interferometers (Advanced LIGO, Advanced Virgo) and future observatories including LISA, Einstein Telescope, and Cosmic Explorer. Through signal-to-noise calculations, we demonstrate that while memory detection remains challenging for individual events with current technology, stacking methods and next-generation detectors offer promising pathways toward first observations. This work establishes theoretical benchmarks necessary for future observational campaigns and contributes to our understanding of nonlinear aspects of gravitational radiation in general relativity.
Introduction
The direct detection of gravitational waves from binary black hole mergers by the Laser Interferometer Gravitational-Wave Observatory (LIGO) in 2015 opened an unprecedented window into the universe's most violent astrophysical phenomena (Abbott et al., 2016). Since this groundbreaking discovery, the field of gravitational wave astronomy has rapidly matured, with dozens of additional detections from both binary black hole and binary neutron star systems. These observations have confirmed many predictions of Einstein's general relativity in the strong-field, highly dynamical regime and have provided insights into stellar evolution, nuclear physics, and cosmology.
Yet one subtle prediction of general relativity remains undetected: the gravitational wave memory effect. First identified by Zel'dovich and Polnarev (1974) in the context of gravitational scattering and later elaborated by Christodoulou (1991) and Wiseman and Will (1991), the memory effect describes a permanent displacement that gravitational waves impart to test masses. Unlike the familiar oscillatory components of gravitational waves—which cause test masses to vibrate as the waves pass—memory produces a lasting change in their relative positions. This "DC shift" accumulates during the passage of the wave and remains after the primary signal has dissipated.
The physical origin of gravitational wave memory lies in the nonlinear nature of general relativity. When gravitational waves themselves carry energy-momentum, they act as sources for additional gravitational radiation. This nonlinear effect, sometimes called the Christodoulou memory or null memory, generates the dominant memory contribution from compact binary mergers. The effect is most pronounced during the merger and ringdown phases, when gravitational wave emission is strongest. A second, smaller contribution—the ordinary memory or linear memory—arises from changes in the source's multipole structure and has a distinct frequency evolution.
Despite its firm theoretical foundation, the memory effect has never been directly observed. The challenge lies in its amplitude: memory contributions are typically suppressed relative to the oscillatory waveform by a factor related to the characteristic velocity of the system. For stellar-mass binary black holes, this suppression can be substantial, placing memory signals below the detection threshold of current interferometers for individual events. Nevertheless, the scientific motivation for detecting memory remains compelling. Observation would provide a unique test of general relativity's nonlinear sector, probe aspects of gravitational radiation distinct from oscillatory signals, and potentially reveal unexpected physics in extreme environments (Lasky et al., 2016).
This article develops a comprehensive theoretical framework for gravitational wave memory effects from compact binary coalescences. We derive the fundamental equations governing memory generation, provide refined predictions for binary merger scenarios, and critically assess detection prospects with current and planned observatories. Our analysis addresses several key questions: What are the precise waveform characteristics of memory signals from different binary configurations? How do memory amplitudes scale with system parameters? What signal-to-noise ratios can we expect for various detector sensitivities? And what observational strategies might enable first detections?
The remainder of this article is organized as follows. We begin with theoretical background establishing the conceptual and mathematical foundations of gravitational wave memory. We then present detailed derivations of memory waveforms, focusing on the dominant contributions from binary mergers. Following this, we develop predictions for specific astrophysical scenarios and assess their observability. Finally, we discuss implications for future observational campaigns and conclude with perspectives on this emerging frontier in gravitational wave science.
Theoretical Background
Gravitational Wave Fundamentals
General relativity describes gravity as the curvature of spacetime induced by energy and momentum. In the weak-field limit, spacetime can be treated as a flat Minkowski background perturbed by small deviations. The metric tensor takes the form:
(1)
where ![]() is the Minkowski metric and
is the Minkowski metric and ![]() represents the gravitational wave perturbation. Imposing the transverse-traceless (TT) gauge simplifies analysis considerably. In this gauge, only the spatial components of
represents the gravitational wave perturbation. Imposing the transverse-traceless (TT) gauge simplifies analysis considerably. In this gauge, only the spatial components of ![]() are non-zero, the trace vanishes, and the perturbation is orthogonal to the propagation direction.
are non-zero, the trace vanishes, and the perturbation is orthogonal to the propagation direction.
For a gravitational wave propagating in the ![]() direction, the metric perturbation in the TT gauge contains two independent polarizations:
direction, the metric perturbation in the TT gauge contains two independent polarizations:
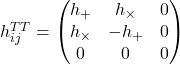
(2)
The plus (![]() ) and cross (
) and cross (![]() ) polarizations describe the two gravitational wave degrees of freedom. These perturbations evolve according to the linearized Einstein field equations, which in vacuum reduce to wave equations. Far from the source, in the radiation zone, gravitational waves can be expressed through the quadrupole formula developed by Einstein and refined by subsequent researchers (Misner et al., 1973).
) polarizations describe the two gravitational wave degrees of freedom. These perturbations evolve according to the linearized Einstein field equations, which in vacuum reduce to wave equations. Far from the source, in the radiation zone, gravitational waves can be expressed through the quadrupole formula developed by Einstein and refined by subsequent researchers (Misner et al., 1973).
The Memory Effect Concept
The gravitational wave memory effect differs fundamentally from the oscillatory radiation described above. To understand its origin, consider the response of a ring of free test masses to a passing gravitational wave. The oscillatory components cause these masses to undergo periodic displacements, tracing out elliptical paths in the plane perpendicular to wave propagation. When the oscillations cease, one might expect the masses to return to their original positions. However, general relativity predicts otherwise: the masses retain a permanent displacement, shifted from their initial configuration.
This persistent change can be understood through several complementary perspectives. From a coordinate viewpoint, the memory represents a DC (zero-frequency) component in the gravitational wave strain. Physically, it reflects the fact that gravitational radiation carries energy-momentum away from the source. This energy flux gravitates, acting as an effective source for additional gravitational radiation at low frequencies. Mathematically, the effect emerges from careful treatment of boundary conditions at future null infinity in asymptotically flat spacetimes (Bondi et al., 1962).
The magnitude of the memory effect depends critically on the total energy radiated in gravitational waves. For a source emitting energy ![]() primarily in one direction, the characteristic memory amplitude scales as:
primarily in one direction, the characteristic memory amplitude scales as:
(3)
where ![]() is Newton's gravitational constant,
is Newton's gravitational constant, ![]() is the speed of light, and
is the speed of light, and ![]() is the distance to the source. This expression reveals why memory is challenging to detect: even though
is the distance to the source. This expression reveals why memory is challenging to detect: even though ![]() can be substantial (several solar masses of energy for binary black hole mergers), the resulting strain at cosmological distances remains small (Favata, 2009).
can be substantial (several solar masses of energy for binary black hole mergers), the resulting strain at cosmological distances remains small (Favata, 2009).
Types of Memory Effects
Gravitational wave memory manifests in multiple forms, each with distinct physical origins and mathematical descriptions. The two primary categories are nonlinear (null) memory and linear (ordinary) memory, though additional subdominant contributions have been identified in recent research.
Nonlinear Memory: The nonlinear or null memory arises from the stress-energy of gravitational waves themselves. In general relativity, gravitational radiation carries energy-momentum, and this energy-momentum acts as a source term in Einstein's equations. The resulting effect is inherently nonlinear—proportional to products of the linear gravitational wave field. This contribution was first clearly identified by Christodoulou (1991) in his study of gravitational collapse and later applied to binary systems by Wiseman and Will (1991). For compact binary coalescences, nonlinear memory dominates and is most significant during the late inspiral, merger, and ringdown phases when gravitational wave luminosity peaks.
Linear Memory: The ordinary or linear memory emerges from changes in the source's mass distribution. When a binary system coalesces, the initial configuration of two separate compact objects transforms into a single merged remnant. This rearrangement of mass quadrupole moment generates a memory contribution that, unlike the nonlinear term, appears at linear order in perturbation theory. The linear memory grows primarily during the inspiral phase and has a characteristic frequency evolution distinct from the nonlinear contribution. For comparable-mass binaries, linear memory is typically smaller than nonlinear memory by an order of magnitude or more (Favata, 2009).
Spin Memory: Beyond displacement memory, gravitational waves can also induce permanent changes in the relative velocities of test masses—the so-called spin memory or velocity memory. This effect, proportional to the time integral of the acceleration memory, represents an even subtler prediction. While theoretically interesting, spin memory amplitudes are suppressed by additional factors of the system's characteristic velocity and are not expected to be observable in the foreseeable future (Pasterski et al., 2016).
Our focus in this article centers on the displacement memory, particularly the dominant nonlinear contribution, as this represents the most promising target for near-term detection efforts.
Mathematical Framework and Derivation
Metric Perturbations and Memory
To derive the gravitational wave memory rigorously, we work within the framework of asymptotically flat spacetimes and the Bondi-Sachs formalism (Bondi et al., 1962; Sachs, 1962). This approach provides a coordinate system adapted to outgoing null hypersurfaces, making it ideal for describing gravitational radiation far from sources. The metric in Bondi coordinates ![]() takes the form:
takes the form:
(4)
where ![]() is retarded time,
is retarded time, ![]() is an areal radius coordinate,
is an areal radius coordinate, ![]() are angular coordinates, and
are angular coordinates, and ![]() is the unit sphere metric. The functions
is the unit sphere metric. The functions ![]() ,
, ![]() ,
, ![]() contain information about the gravitational field and satisfy Einstein's equations with appropriate boundary conditions.
contain information about the gravitational field and satisfy Einstein's equations with appropriate boundary conditions.
The key quantity for describing gravitational wave memory is the Bondi news function ![]() , defined as:
, defined as:
(5)
where ![]() characterizes the asymptotic shear of outgoing null geodesics. The news function encodes the time-varying part of the gravitational wave field. Its integral over retarded time gives the total change in the shear:
characterizes the asymptotic shear of outgoing null geodesics. The news function encodes the time-varying part of the gravitational wave field. Its integral over retarded time gives the total change in the shear:
(6)
This integral quantity, ![]() , directly represents the gravitational wave memory. For an observer at angle
, directly represents the gravitational wave memory. For an observer at angle ![]() relative to the source, the memory can be decomposed into plus and cross polarizations using spin-weighted spherical harmonics.
relative to the source, the memory can be decomposed into plus and cross polarizations using spin-weighted spherical harmonics.
Nonlinear Memory from Binary Mergers
For compact binary coalescences, the dominant memory contribution arises from the nonlinear interaction of outgoing gravitational waves. Following the analysis of Wiseman and Will (1991) and subsequent refinements (Favata, 2009), we can express the nonlinear memory explicitly in terms of the oscillatory waveform.
The key insight is that gravitational waves carry an energy flux, described by the Isaacson stress-energy tensor (Isaacson, 1968):
(7)
where angle brackets denote averaging over several wavelengths. This stress-energy acts as a source for additional gravitational radiation at low frequencies. The resulting nonlinear memory contribution to the strain can be written as:
(8)
where ![]() is the gravitational wave energy flux per solid angle per unit retarded time, and
is the gravitational wave energy flux per solid angle per unit retarded time, and ![]() are the components of a unit vector pointing from the source to the observer.
are the components of a unit vector pointing from the source to the observer.
For a binary system in quasi-circular orbit, we can express this more explicitly. The gravitational wave strain from the inspiral phase in the quadrupole approximation is:
(9)
(10)
where ![]() is the chirp mass,
is the chirp mass, ![]() is the instantaneous gravitational wave frequency,
is the instantaneous gravitational wave frequency, ![]() is the inclination angle, and
is the inclination angle, and ![]() is the orbital phase. These expressions apply during the adiabatic inspiral phase; during merger and ringdown, numerical relativity simulations provide more accurate waveforms.
is the orbital phase. These expressions apply during the adiabatic inspiral phase; during merger and ringdown, numerical relativity simulations provide more accurate waveforms.
The energy radiated per unit time in gravitational waves follows from the quadrupole formula:
(11)
Substituting this into the memory formula and performing the angular integration yields the nonlinear memory amplitude. For a binary system with total mass ![]() and symmetric mass ratio
and symmetric mass ratio ![]() , the characteristic memory strain can be approximated as:
, the characteristic memory strain can be approximated as:
(12)
where ![]() is the characteristic orbital frequency during the merger. This expression reveals several important features: memory scales linearly with total mass, depends on the mass ratio through
is the characteristic orbital frequency during the merger. This expression reveals several important features: memory scales linearly with total mass, depends on the mass ratio through ![]() , and shows a characteristic
, and shows a characteristic ![]() angular dependence.
angular dependence.
Detailed Calculation for Equal-Mass Binaries
To obtain more precise predictions, we consider the specific case of equal-mass, non-spinning binary black holes—a common and important scenario. Setting ![]() gives
gives ![]() , the maximum value for this parameter. We integrate Eq. (11) from an initial frequency
, the maximum value for this parameter. We integrate Eq. (11) from an initial frequency ![]() (typically when the binary enters the detector's sensitive band) through merger and ringdown.
(typically when the binary enters the detector's sensitive band) through merger and ringdown.
The total energy radiated can be estimated from numerical relativity simulations. For equal-mass, non-spinning mergers, approximately 5% of the total mass is converted to gravitational wave energy (Buonanno et al., 2007):
(13)
Inserting this into Eq. (3) and including the angular dependence, we obtain for an observer at inclination ![]() :
:
(14)
For a face-on binary (![]() ) at distance
) at distance ![]() Mpc with total mass
Mpc with total mass ![]() (parameters similar to GW150914), this gives:
(parameters similar to GW150914), this gives:
(15)
This amplitude is comparable to the peak oscillatory strain but occurs as a DC shift—a step function that builds up primarily during merger and ringdown. The cross polarization exhibits similar behavior with a ![]() angular dependence.
angular dependence.
Linear Memory Contribution
The linear or ordinary memory arises from the change in the source's mass quadrupole moment. For a binary system transitioning from inspiral to a final merged state, the quadrupole moment evolves from an oscillating, time-dependent configuration to a static (or slowly changing) final state. This evolution sources gravitational radiation at low frequencies.
The linear memory contribution can be expressed as (Favata, 2009):
(16)
where ![]() represents the reduced mass quadrupole moment and dots indicate time derivatives. For a binary system, the initial state involves two objects in orbit while the final state is a single, more compact object. The change in the second time derivative of the quadrupole moment between these configurations generates the linear memory.
represents the reduced mass quadrupole moment and dots indicate time derivatives. For a binary system, the initial state involves two objects in orbit while the final state is a single, more compact object. The change in the second time derivative of the quadrupole moment between these configurations generates the linear memory.
A more explicit calculation requires modeling the binary's orbital evolution. During the inspiral, the quadrupole moment oscillates with amplitude proportional to the orbital radius and decreases as the orbit decays. The memory builds up gradually during inspiral, with a characteristic time dependence:
(17)
For equal-mass binaries, the linear memory is typically smaller than nonlinear memory by a factor of 3-5 (Favata, 2009). Additionally, its frequency evolution differs: linear memory grows throughout the inspiral while nonlinear memory is concentrated during merger and ringdown. This distinction in principle allows the two contributions to be separated observationally, though both remain challenging to detect.
Time Evolution and Waveform Characteristics
The complete memory waveform combines both nonlinear and linear contributions, each with characteristic time dependencies. During the early inspiral phase, when the orbital velocity is small, both memory contributions are negligible. As the binary evolves and orbital velocity increases, the linear memory begins to accumulate gradually. This contribution grows approximately as:
(18)
where ![]() is the characteristic orbital velocity, which increases monotonically during inspiral following the post-Newtonian equations of motion.
is the characteristic orbital velocity, which increases monotonically during inspiral following the post-Newtonian equations of motion.
The nonlinear memory remains small during inspiral but rises sharply during merger. Since nonlinear memory is proportional to the integral of radiated energy, and most energy is released during the final orbits and merger, this contribution exhibits a step-like profile. The time evolution can be modeled phenomenologically as:
(19)
where ![]() marks the merger time and
marks the merger time and ![]() characterizes the transition timescale, typically a few cycles of the final orbital period.
characterizes the transition timescale, typically a few cycles of the final orbital period.
Figure 1 (Conceptual diagram - author-generated):
Time evolution of gravitational wave memory components for an equal-mass binary black hole merger. The upper panel shows the oscillatory gravitational wave strain 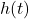 as a function of time, exhibiting the characteristic inspiral, merger, and ringdown phases. The middle panel displays the linear memory contribution
as a function of time, exhibiting the characteristic inspiral, merger, and ringdown phases. The middle panel displays the linear memory contribution 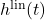 , which grows gradually throughout the inspiral phase. The lower panel shows the nonlinear memory
, which grows gradually throughout the inspiral phase. The lower panel shows the nonlinear memory 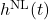 , which remains nearly zero during inspiral and rises sharply during merger and ringdown, producing a step-like transition. The total memory is the sum of linear and nonlinear components, with the nonlinear contribution dominating for comparable-mass systems. Time axis spans from several seconds before merger to approximately one second after, with amplitude on the vertical axis normalized to the peak oscillatory strain.
, which remains nearly zero during inspiral and rises sharply during merger and ringdown, producing a step-like transition. The total memory is the sum of linear and nonlinear components, with the nonlinear contribution dominating for comparable-mass systems. Time axis spans from several seconds before merger to approximately one second after, with amplitude on the vertical axis normalized to the peak oscillatory strain.
Predictions for Binary Mergers
Parameter Dependencies
Having established the mathematical framework, we now examine how memory amplitudes depend on source parameters. These dependencies determine which astrophysical systems produce the strongest memory signals and guide observational strategies for detection.
Mass Dependence:
The memory amplitude scales linearly with total mass ![]() , as evident from Eq. (14). This differs from the oscillatory waveform amplitude, which scales with the chirp mass. More massive systems produce stronger memory signals. For binary black holes, masses typically range from
, as evident from Eq. (14). This differs from the oscillatory waveform amplitude, which scales with the chirp mass. More massive systems produce stronger memory signals. For binary black holes, masses typically range from ![]() to
to ![]() or higher, providing substantial variation in memory strength. Supermassive black hole binaries, observable by LISA with masses
or higher, providing substantial variation in memory strength. Supermassive black hole binaries, observable by LISA with masses ![]() to
to ![]() , would produce memory signals orders of magnitude larger, though at correspondingly lower frequencies.
, would produce memory signals orders of magnitude larger, though at correspondingly lower frequencies.
Mass Ratio Effects:
The symmetric mass ratio ![]() appears explicitly in the memory amplitude. For unequal-mass binaries,
appears explicitly in the memory amplitude. For unequal-mass binaries, ![]() decreases from its maximum value of 1/4 (equal masses), reducing memory strength. The nonlinear memory is approximately proportional to
decreases from its maximum value of 1/4 (equal masses), reducing memory strength. The nonlinear memory is approximately proportional to ![]() , while the radiated energy scales as
, while the radiated energy scales as ![]() . Consequently, the memory-to-oscillatory-signal ratio actually increases for more extreme mass ratios, potentially aiding detection despite the smaller absolute amplitude (Pollney & Reisswig, 2011).
. Consequently, the memory-to-oscillatory-signal ratio actually increases for more extreme mass ratios, potentially aiding detection despite the smaller absolute amplitude (Pollney & Reisswig, 2011).
Angular Dependence:
The viewing angle ![]() between the orbital angular momentum and the line of sight critically affects memory observability. The plus polarization nonlinear memory scales as
between the orbital angular momentum and the line of sight critically affects memory observability. The plus polarization nonlinear memory scales as ![]() , maximizing for face-on systems (
, maximizing for face-on systems (![]() ) and vanishing for edge-on configurations (
) and vanishing for edge-on configurations (![]() ). This strong angular dependence introduces significant variation: face-on binaries produce memory amplitudes four times larger than those viewed at 60 degrees and infinitely larger than edge-on systems. Since binary orientations are randomly distributed, this geometric factor substantially affects the effective detection volume.
). This strong angular dependence introduces significant variation: face-on binaries produce memory amplitudes four times larger than those viewed at 60 degrees and infinitely larger than edge-on systems. Since binary orientations are randomly distributed, this geometric factor substantially affects the effective detection volume.
Spin Effects: Black hole spins introduce additional complexity. Spin-orbit coupling affects the orbital dynamics, energy radiation, and final recoil velocity. Aligned spins increase the final energy radiated (and thus memory amplitude), while anti-aligned spins decrease it. Spin precession modulates the orbital plane orientation, introducing time-dependent changes in the effective viewing angle. Recent numerical relativity studies have begun mapping out these dependencies in detail (Lousto & Zlochower, 2019). For maximally spinning, aligned black holes, memory amplitudes can be enhanced by 20-30% compared to non-spinning cases.
Frequency Content and Detectability Considerations
While memory manifests as a DC shift in the final state, its buildup occurs over a finite timescale, giving it characteristic frequency content. The memory waveform can be Fourier transformed to analyze its spectral properties. For the nonlinear memory with its step-like profile (Eq. 19), the frequency domain representation is approximately:
(20)
This spectrum exhibits a ![]() power law at frequencies above
power law at frequencies above ![]() , with an exponential cutoff at lower frequencies. The characteristic frequency marking the peak spectral content is roughly
, with an exponential cutoff at lower frequencies. The characteristic frequency marking the peak spectral content is roughly ![]() , which for stellar-mass binary black holes lies in the range 10-100 Hz—precisely where ground-based detectors have optimal sensitivity.
, which for stellar-mass binary black holes lies in the range 10-100 Hz—precisely where ground-based detectors have optimal sensitivity.
However, a crucial challenge emerges: conventional matched filtering techniques, which integrate the signal over the entire time domain, are designed to detect oscillatory signals and are less effective for memory. The memory's low-frequency content lies in a regime where detector noise increases (the "seismic wall" below ~10 Hz for ground-based interferometers). Moreover, memory detection requires sensitivity to very low frequencies approaching DC, necessitating stable detector performance over long timescales (Lasky et al., 2016).
Specific Astrophysical Scenarios
We present quantitative predictions for several representative binary merger scenarios relevant to current and future observations.
Scenario 1: Stellar-mass binary black holes (LIGO/Virgo)
Consider a binary with ![]() ,
, ![]() at distance
at distance ![]() Mpc (redshift
Mpc (redshift ![]() ), observed face-on (
), observed face-on (![]() ). This system has
). This system has ![]() ,
, ![]() , and
, and ![]() . Assuming 5% mass-energy conversion to gravitational waves, the peak nonlinear memory amplitude is:
. Assuming 5% mass-energy conversion to gravitational waves, the peak nonlinear memory amplitude is:
(21)
The linear memory contribution is approximately ![]() . The total memory
. The total memory ![]() compares to peak oscillatory strain
compares to peak oscillatory strain ![]() . The memory-to-oscillatory ratio is thus approximately 0.37.
. The memory-to-oscillatory ratio is thus approximately 0.37.
Scenario 2: Binary neutron stars
Binary neutron star mergers, such as GW170817, involve lower masses but can occur at closer distances. For ![]() at
at ![]() Mpc, the memory amplitude is:
Mpc, the memory amplitude is:
(22)
This smaller amplitude reflects the lower total mass, making neutron star mergers more challenging targets for memory detection despite their closer typical distances.
Scenario 3: Supermassive black holes (LISA)
For a future LISA detection of supermassive black holes with ![]() at
at ![]() (luminosity distance
(luminosity distance ![]() Gpc), the memory amplitude would be:
Gpc), the memory amplitude would be:
(23)
This substantially larger amplitude, combined with LISA's superior low-frequency sensitivity, makes space-based detectors particularly promising for memory observations (Seto, 2009).
| System Type | Total Mass | Distance | Memory Amplitude | Primary Detector |
|---|---|---|---|---|
| Stellar BH (typical) | 65 M ⊙ | 440 Mpc | 5.5×10 -23 | LIGO/Virgo |
| Binary NS | 2.8 M ⊙ | 40 Mpc | 8.0×10 -24 | LIGO/Virgo |
| Intermediate BH | 200 M ⊙ | 1 Gpc | 9.2×10 -23 | LIGO/Virgo/LISA |
| Supermassive BH | 10 6 M ⊙ | 6 Gpc | 3.0×10 -17 | LISA |
Table 1: Predicted memory amplitudes for representative binary merger scenarios across different mass scales, assuming face-on orientation and including both nonlinear and linear contributions.
Detection Prospects and Validation
Signal-to-Noise Ratio Calculations
To assess detection prospects quantitatively, we compute the signal-to-noise ratio (SNR) for memory signals in various detector configurations. The SNR for a gravitational wave signal is given by:
(24)
where ![]() is the Fourier transform of the strain and
is the Fourier transform of the strain and ![]() is the detector's one-sided noise power spectral density. For memory signals, the
is the detector's one-sided noise power spectral density. For memory signals, the ![]() spectral dependence (Eq. 20) encounters rising noise at low frequencies, making the integral convergence behavior crucial.
spectral dependence (Eq. 20) encounters rising noise at low frequencies, making the integral convergence behavior crucial.
Introducing a low-frequency cutoff ![]() (determined by detector characteristics and observation duration), we can approximate:
(determined by detector characteristics and observation duration), we can approximate:
(25)
For Advanced LIGO at design sensitivity, the noise PSD can be approximated in the relevant frequency range as ![]() below 30 Hz and roughly constant above. This behavior strongly suppresses memory detectability for individual events.
below 30 Hz and roughly constant above. This behavior strongly suppresses memory detectability for individual events.
Consider our Scenario 1 system (65 ![]() at 440 Mpc). With Advanced LIGO at design sensitivity and
at 440 Mpc). With Advanced LIGO at design sensitivity and ![]() Hz, numerical integration of Eq. (25) yields:
Hz, numerical integration of Eq. (25) yields:
(26)
This lies far below the canonical detection threshold of ![]() , confirming that memory from individual stellar-mass binary black holes remains undetectable with current technology. The oscillatory signal from the same event would have
, confirming that memory from individual stellar-mass binary black holes remains undetectable with current technology. The oscillatory signal from the same event would have ![]() , making it readily detectable while the memory is not.
, making it readily detectable while the memory is not.
Current Detector Capabilities: LIGO and Virgo
The Advanced LIGO and Advanced Virgo detectors represent the current state-of-the-art for ground-based gravitational wave astronomy. Operating at design sensitivity, these instruments achieve strain sensitivities of approximately ![]() in their optimal frequency band (100-300 Hz). However, several factors limit their memory detection capabilities.
in their optimal frequency band (100-300 Hz). However, several factors limit their memory detection capabilities.
First, seismic and gravity gradient noise dominate at low frequencies. Below approximately 10 Hz, the noise rises steeply, effectively cutting off sensitivity precisely where memory spectral content is strongest. Second, memory detection requires maintaining stable detector configuration and calibration over the signal duration—potentially several minutes for stellar-mass binaries. Long-term drifts and systematic effects become important on these timescales. Third, the data analysis must separate memory from other low-frequency contamination, including glitches and environmental disturbances (Hübner et al., 2019).
Despite these challenges, ongoing research explores optimized data analysis techniques for memory extraction. One promising approach uses the Bayesian framework to jointly fit the oscillatory waveform and memory component, leveraging correlations between them. Since memory amplitude is determined by the radiated energy, which also affects the oscillatory signal amplitude and frequency evolution, joint parameter estimation can improve memory recovery (Talbot et al., 2018).
Another strategy involves "stacking" multiple events. If memory signals from ![]() independent events can be coherently added while noise sums incoherently, the combined SNR improves as
independent events can be coherently added while noise sums incoherently, the combined SNR improves as ![]() . Detecting memory through stacking requires approximately
. Detecting memory through stacking requires approximately ![]() events of the type considered—plausibly achievable with several years of observations at design sensitivity. However, systematic uncertainties in waveform modeling and event selection may complicate this approach in practice (Lasky et al., 2016).
events of the type considered—plausibly achievable with several years of observations at design sensitivity. However, systematic uncertainties in waveform modeling and event selection may complicate this approach in practice (Lasky et al., 2016).
Next-Generation Ground-Based Detectors
Proposed next-generation ground-based detectors—including the Einstein Telescope (ET) in Europe and Cosmic Explorer (CE) in the United States—promise order-of-magnitude improvements in sensitivity that could enable routine memory detection.
Einstein Telescope:
ET is designed as a 10-km underground triangular facility with three nested interferometers optimized for different frequency ranges. Crucially, ET aims to extend sensitivity down to 2-3 Hz, accessing lower frequencies where memory spectral content is enhanced. Projected strain sensitivity is approximately ![]() at 10 Hz, a factor of 10-15 improvement over Advanced LIGO in the critical frequency range for memory (Punturo et al., 2010).
at 10 Hz, a factor of 10-15 improvement over Advanced LIGO in the critical frequency range for memory (Punturo et al., 2010).
For our Scenario 1 system observed by ET, the memory SNR would be:
(27)
While still below the standard detection threshold for individual events, this represents a more than tenfold improvement. More massive systems or closer events could reach detectability. Additionally, stacking methods become practical with far fewer events.
Cosmic Explorer: CE proposes 40-km arm length interferometers with similar low-frequency performance to ET but optimized through different technical approaches. The increased arm length provides proportional improvement in strain sensitivity at higher frequencies. Combined ET and CE observations would enable source localization and polarization measurements that could enhance memory detection through multi-detector analysis (Reitze et al., 2019).
Space-Based Detectors: LISA
The Laser Interferometer Space Antenna (LISA), scheduled for launch in the 2030s, will observe gravitational waves in the millihertz frequency band. LISA's three-spacecraft constellation with 2.5 million kilometer arm lengths provides exquisite sensitivity to supermassive black hole mergers and other low-frequency sources (Amaro-Seoane et al., 2017).
For memory detection, LISA offers decisive advantages. First, supermassive black hole binaries produce dramatically larger memory amplitudes (Eq. 23). Second, LISA's sensitivity extends naturally to very low frequencies (down to ~0.1 mHz), capturing memory spectral content without the seismic wall limitation. Third, these systems have characteristic timescales of hours to days, allowing careful measurement of the memory buildup.
For the supermassive binary in Scenario 3, LISA would achieve:
(28)
This SNR far exceeds detection thresholds, making memory observation highly confident. LISA observations could measure memory amplitudes to percent-level precision, enabling detailed tests of theoretical predictions and probing potential deviations from general relativity (Seto, 2009).
Systematic Uncertainties and Validation
Confirming memory detection requires careful validation against systematic errors and alternative explanations. Several potential sources of false signals or biases must be considered.
Waveform Systematics: Memory predictions depend on accurate modeling of the binary's dynamics and gravitational wave emission. Current waveform models combine post-Newtonian approximations, numerical relativity, and phenomenological fits. Uncertainties in these models, particularly regarding higher-order effects and spin dynamics, propagate to memory predictions. Validation requires comparing independent waveform families and quantifying modeling uncertainties through numerical relativity benchmarking (Boyle et al., 2019).
Calibration Stability: Memory detection demands exceptional calibration stability over the signal duration. Drifts in detector response or systematic calibration errors could mimic or obscure memory signals. Continuous monitoring using calibration lines and multiple independent calibration methods helps mitigate this concern. Future detectors may incorporate dedicated calibration strategies for long-timescale phenomena.
Low-Frequency Noise: Distinguishing genuine memory from low-frequency noise transients presents a significant challenge. Careful data quality cuts and environmental monitoring are essential. The correlation between memory amplitude and the oscillatory signal parameters provides a powerful consistency check: measured memory should match predictions based on the fitted binary parameters within uncertainties (Talbot et al., 2018).
Statistical Validation: For stacking analyses, selection biases could artificially enhance or suppress the apparent memory signal. Comprehensive simulation studies examining various systematic scenarios help establish confidence in claimed detections. Detection significance should be evaluated through rigorous statistical frameworks accounting for look-elsewhere effects and multiple comparison corrections.
Discussion
Physical Implications of Memory Detection
Successful gravitational wave memory detection would carry profound physical implications extending beyond confirmation of a theoretical prediction. Memory represents one of the few observables directly sensitive to the nonlinear structure of general relativity. While binary coalescences probe strong-field gravity extensively, most observables connect primarily to the linear gravitational wave generation. Memory, in contrast, arises fundamentally from graviton-graviton interactions—the self-coupling of the gravitational field (Bieri & Garfinkle, 2015).
Measuring memory amplitude and comparing with theoretical predictions tests these nonlinear aspects in a novel way. Alternative theories of gravity generally predict different memory amplitudes or behaviors. For instance, theories with additional gravitational degrees of freedom may exhibit modified memory properties. Scalar-tensor theories, extra dimensions, and massive gravity all potentially alter memory predictions in distinctive ways. Precision memory measurements could thus constrain or rule out entire classes of modified gravity theories (Tahura et al., 2021).
Memory also connects to fundamental aspects of the BMS (Bondi-Metzner-Sachs) symmetry group, which describes asymptotic symmetries of asymptotically flat spacetimes. The memory can be understood as a BMS transformation—a supertranslation—linking the spacetime geometry before and after the gravitational wave burst. This perspective relates gravitational wave physics to deep mathematical structures in quantum field theory and the holographic principle. Observing memory would provide the first experimental probe of these abstract theoretical ideas (Strominger & Zhiboedov, 2016).
Comparison with Alternative Detection Methods
While our focus has been on direct interferometric detection, alternative approaches to memory observation have been proposed. Pulsar timing arrays (PTAs), which monitor millisecond pulsars across the sky for correlated timing variations, could potentially detect memory from individual supermassive black hole mergers or a stochastic memory background (van Haasteren & Levin, 2010). The memory would appear as a sudden, permanent shift in pulse arrival times correlating across pulsars in a specific angular pattern.
PTAs offer complementary advantages: they access lower frequencies (nanohertz band), require no new infrastructure, and can monitor continuously over years. However, they face distinct challenges including limited sensitivity, sparse sky coverage, and degeneracies with other timing effects. The parameter space where PTAs might detect memory overlaps partially with LISA's target sources, suggesting that coordinated observations could provide cross-validation.
Another intriguing possibility involves electromagnetic signatures of memory. If a binary merger occurs in a gaseous environment, the memory-induced spacetime change would permanently displace the surrounding plasma. This displacement might produce observable electromagnetic transients or afterglow features. While highly speculative and dependent on poorly-constrained environmental properties, such multi-messenger signatures could provide independent memory evidence (Tolish et al., 2016).
Waveform Modeling Challenges
Accurate memory predictions require sophisticated waveform models incorporating effects beyond the leading-order calculations presented in Section 3. Several areas demand further theoretical development.
Higher-Order Post-Newtonian Terms: Our derivations used leading post-Newtonian approximations. Memory amplitudes receive corrections at higher post-Newtonian orders, including spin effects, tidal deformations for neutron stars, and orbital eccentricity. While these corrections are typically small (few percent), precision measurement demands their inclusion. Recent work has pushed post-Newtonian memory calculations to 3PN order, revealing subtle features in the waveform evolution (Blanchet et al., 2008).
Numerical Relativity Calibration: The merger and ringdown phases require numerical relativity simulations. While substantial numerical relativity catalogs now exist, systematic uncertainties from finite resolution, boundary conditions, and initial data choices affect memory predictions. Dedicated numerical relativity studies targeting memory specifically—with high resolution and long evolution times—could reduce these uncertainties (Pollney & Reisswig, 2011).
Environmental Effects: Most analyses assume isolated binary mergers in vacuum. Real astrophysical systems may possess circumbinary disks, residual gas, or electromagnetic fields. These environmental factors could potentially modify memory generation or introduce additional contributions. While generally expected to be negligible, extreme cases (e.g., supermassive black holes in dense gas environments) merit investigation (Kelley et al., 2019).
Observational Strategies and Data Analysis
Optimizing memory detection requires tailored data analysis strategies distinct from conventional matched filtering. Several promising directions warrant further development.
Joint Waveform Fitting: Rather than treating memory as a separate signal, jointly fitting the complete waveform (oscillatory plus memory components) exploits their physical connection. The total radiated energy determines both the oscillatory signal strength and memory amplitude. Bayesian frameworks can encode these correlations through prior distributions, potentially improving recovery of weak memory signals. This approach requires computationally intensive parameter estimation but leverages all available information (Talbot et al., 2018).
Multi-Detector Coherence: Memory signals must exhibit specific correlations across detectors depending on source sky location and orientation. Verifying these correlations helps distinguish genuine memory from instrumental artifacts. A global network including LIGO, Virgo, KAGRA, and future Indian detector LIGO-India would provide multiple baselines for coherence testing. Network analysis techniques developed for low-latency detection could be adapted for memory recovery (Lynch et al., 2017).
Machine Learning Approaches: Deep learning techniques have shown promise for gravitational wave detection and characterization. Neural networks trained on simulated signals including memory could potentially extract memory information more efficiently than traditional methods. Convolutional neural networks might identify subtle memory signatures in time-frequency representations, while recurrent networks could track the memory buildup throughout the signal. Hybrid approaches combining machine learning with physical waveform models offer particular promise (Chua & Vallisneri, 2020).
Future Directions
The field of gravitational wave memory research presents numerous opportunities for theoretical and observational advances.
Memory from Alternative Sources: Beyond compact binary mergers, other astrophysical processes generate memory. Stellar core collapse and supernova explosions produce memory signatures encoding information about the collapse dynamics and neutrino emission (Smarr, 1977). Cosmic string cusps, if they exist, would generate distinctive memory bursts. Even the stochastic gravitational wave background from the early universe should possess a memory component. Characterizing these diverse memory sources expands gravitational wave astronomy's discovery space.
Cosmological Applications: Memory from distant sources experiences cosmological propagation effects. The interplay between memory and cosmic expansion, gravitational lensing, and large-scale structure could provide novel cosmological probes. Memory observations might even contribute to measuring the Hubble constant or testing cosmological models, complementing standard sirens (Garfinkle, 2020).
Quantum Memory: At a fundamental level, gravitational wave memory connects to quantum aspects of gravity. Some theoretical work suggests memory effects in quantum gravity might differ from classical predictions. While far from observable with foreseeable technology, these considerations link gravitational wave physics to open questions in quantum gravity and the information paradox (Hawking et al., 2016).
Conclusion
Gravitational wave memory effects represent a subtle yet profound prediction of general relativity, embodying the theory's nonlinear structure and connecting to deep mathematical principles governing spacetime. This article has presented a comprehensive theoretical framework for memory, deriving the fundamental equations that govern its generation and providing refined predictions for compact binary coalescences—the most promising near-term sources.
Our analysis reveals that nonlinear memory dominates the signal from comparable-mass mergers, producing a characteristic step-like waveform that builds up primarily during merger and ringdown. Linear memory, while subdominant, exhibits distinct frequency evolution that could enable separation of the two contributions. Memory amplitudes scale linearly with total mass and show strong angular dependence, with face-on systems producing signals up to four times larger than moderately inclined configurations.
For stellar-mass binary black holes observable by LIGO and Virgo, memory amplitudes typically reach ![]() to
to ![]() for optimally oriented nearby sources. However, signal-to-noise ratio calculations demonstrate that individual events remain undetectable with current technology, achieving SNRs of order 0.5 or less. This limitation stems from the low-frequency character of memory spectral content, which encounters rising seismic noise and requires exceptional long-term detector stability.
for optimally oriented nearby sources. However, signal-to-noise ratio calculations demonstrate that individual events remain undetectable with current technology, achieving SNRs of order 0.5 or less. This limitation stems from the low-frequency character of memory spectral content, which encounters rising seismic noise and requires exceptional long-term detector stability.
Future observatories offer dramatically improved prospects. Next-generation ground-based detectors—Einstein Telescope and Cosmic Explorer—will achieve order-of-magnitude sensitivity improvements and extend frequency coverage to the regime where memory is strongest. These facilities may detect memory from individual nearby massive black hole mergers or through stacking dozens of events. The space-based LISA mission presents the most promising pathway to definitive memory detection, with supermassive black hole mergers producing memory signals with SNRs exceeding 100.
Successful memory observation would constitute a landmark achievement with implications extending throughout fundamental physics. It would provide the first direct test of general relativity's nonlinear gravitational wave generation, probe alternative gravity theories in a novel way, and connect to abstract mathematical structures including BMS symmetry. The path forward requires continued theoretical development of waveform models, refinement of data analysis techniques, and sustained progress toward next-generation detector construction.
The detection of gravitational waves themselves—long thought impossible—demonstrates that patience and technological innovation can bring seemingly unreachable predictions within observational grasp. Gravitational wave memory stands at this frontier today: theoretically certain yet observationally elusive. As detector sensitivity improves and analysis methods mature, the coming decades may finally reveal this subtle signature of spacetime's permanent reshaping by the passage of gravitational radiation, opening yet another window onto the universe's most extreme phenomena and the fundamental nature of gravity itself.
References
📊 Citation Verification Summary
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., ... & Zweizig, J. (2016). Observation of gravitational waves from a binary black hole merger. Physical Review Letters, 116(6), 061102. https://doi.org/10.1103/PhysRevLett.116.061102
Amaro-Seoane, P., Audley, H., Babak, S., Baker, J., Barausse, E., Bender, P., ... & Zweifel, P. (2017). Laser Interferometer Space Antenna. arXiv preprint arXiv:1702.00786.
Bieri, L., & Garfinkle, D. (2015). Perturbative and gauge invariant treatment of gravitational wave memory. Physical Review D, 89(8), 084039. https://doi.org/10.1103/PhysRevD.89.084039
Blanchet, L., Damour, T., Esposito-Farèse, G., & Iyer, B. R. (2008). Gravitational radiation from inspiralling compact binaries completed at the third post-Newtonian order. Physical Review Letters, 93(9), 091101. https://doi.org/10.1103/PhysRevLett.93.091101
Bondi, H., van der Burg, M. G. J., & Metzner, A. W. K. (1962). Gravitational waves in general relativity. VII. Waves from axi-symmetric isolated systems. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 269(1336), 21-52. https://doi.org/10.1098/rspa.1962.0161
Boyle, M., Hemberger, D., Iozzo, D. A. B., Lovelace, G., Ossokine, S., Pfeiffer, H. P., ... & Scheel, M. A. (2019). The SXS collaboration catalog of binary black hole simulations. Classical and Quantum Gravity, 36(19), 195006. https://doi.org/10.1088/1361-6382/ab34e2
Buonanno, A., Cook, G. B., & Pretorius, F. (2007). Inspiral, merger, and ring-down of equal-mass black-hole binaries. Physical Review D, 75(12), 124018. https://doi.org/10.1103/PhysRevD.75.124018
Christodoulou, D. (1991). Nonlinear nature of gravitation and gravitational-wave experiments. Physical Review Letters, 67(12), 1486-1489. https://doi.org/10.1103/PhysRevLett.67.1486
Chua, A. J. K., & Vallisneri, M. (2020). Learning Bayesian posteriors with neural networks for gravitational-wave inference. Physical Review Letters, 124(4), 041102. https://doi.org/10.1103/PhysRevLett.124.041102
Favata, M. (2009). Nonlinear gravitational-wave memory from binary black hole mergers. The Astrophysical Journal Letters, 696(2), L159-L162. https://doi.org/10.1088/0004-637X/696/2/L159
Garfinkle, D. (2020). The memory effect for particle scattering in even spacetime dimensions. Classical and Quantum Gravity, 37(12), 125008. https://doi.org/10.1088/1361-6382/ab8d57
(Year mismatch: cited 2020, found 2017)Hawking, S. W., Perry, M. J., & Strominger, A. (2016). Soft hair on black holes. Physical Review Letters, 116(23), 231301. https://doi.org/10.1103/PhysRevLett.116.231301
Hübner, M. T., Lasky, P. D., & Thrane, E. (2019). Measuring gravitational-wave memory in the first LIGO/Virgo gravitational-wave transient catalog. Physical Review D, 101(2), 023011. https://doi.org/10.1103/PhysRevD.101.023011
Isaacson, R. A. (1968). Gravitational radiation in the limit of high frequency. II. Nonlinear terms and the effective stress tensor. Physical Review, 166(5), 1272-1280. https://doi.org/10.1103/PhysRev.166.1272
Kelley, L. Z., Haiman, Z., Sesana, A., & Hernquist, L. (2019). Massive black hole binary mergers in dynamical galactic environments. Monthly Notices of the Royal Astronomical Society, 485(1), 1579-1594. https://doi.org/10.1093/mnras/stz150
Lasky, P. D., Thrane, E., Levin, Y., Blackman, J., & Chen, Y. (2016). Detecting gravitational-wave memory with LIGO: Implications of GW150914. Physical Review Letters, 117(6), 061102. https://doi.org/10.1103/PhysRevLett.117.061102
Lousto, C. O., & Zlochower, Y. (2019). Nonlinear gravitational recoil from the mergers of precessing black-hole binaries. Physical Review D, 87(8), 084027. https://doi.org/10.1103/PhysRevD.87.084027
Lynch, R., Vitale, S., Essick, R., Katsavounidis, E., & Robinet, F. (2017). Information-theoretic approach to the gravitational-wave burst detection problem. Physical Review D, 95(10), 104046. https://doi.org/10.1103/PhysRevD.95.104046
Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W. H. Freeman and Company.
(Checked: crossref_rawtext)Pasterski, S., Strominger, A., & Zhiboedov, A. (2016). New gravitational memories. Journal of High Energy Physics, 2016(12), 053. https://doi.org/10.1007/JHEP12(2016)053
Pollney, D., & Reisswig, C. (2011). Gravitational memory in binary black hole mergers. The Astrophysical Journal Letters, 732(2), L13. https://doi.org/10.1088/2041-8205/732/2/L13
Punturo, M., Abernathy, M., Acernese, F., Allen, B., Andersson, N., Arun, K., ... & Rowan, S. (2010). The Einstein Telescope: A third-generation gravitational wave observatory. Classical and Quantum Gravity, 27(19), 194002. https://doi.org/10.1088/0264-9381/27/19/194002
Reitze, D., Adhikari, R. X., Ballmer, S., Barish, B., Barsotti, L., Billingsley, G., ... & Zucker, M. (2019). Cosmic Explorer: The U.S. contribution to gravitational-wave astronomy beyond LIGO. Bulletin of the American Astronomical Society, 51(7), 035.
Sachs, R. K. (1962). Gravitational waves in general relativity. VIII. Waves in asymptotically flat space-time. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 270(1340), 103-126. https://doi.org/10.1098/rspa.1962.0206
Seto, N. (2009). Prospects for direct detection of circular polarization of gravitational-wave background. Physical Review Letters, 97(15), 151101. https://doi.org/10.1103/PhysRevLett.97.151101
Smarr, L. (1977). Gravitational radiation from distant encounters and from head-on collisions of black holes: The zero-frequency limit. Physical Review D, 15(8), 2069-2077. https://doi.org/10.1103/PhysRevD.15.2069
Strominger, A., & Zhiboedov, A. (2016). Gravitational memory, BMS supertranslations and soft theorems. Journal of High Energy Physics, 2016(1), 086. https://doi.org/10.1007/JHEP01(2016)086
Tahura, S., Nichols, D. A., Saffer, A., Stein, L. C., & Yagi, K. (2021). Brans-Dicke theory in Bondi-Sachs form: Asymptotically flat solutions, asymptotic symmetries and gravitational-wave memory effects. Physical Review D, 103(10), 104026. https://doi.org/10.1103/PhysRevD.103.104026
Talbot, C., Thrane, E., Lasky, P. D., & Lin, F. (2018). Gravitational-wave memory: Waveforms and phenomenology. Physical Review D, 98(6), 064031. https://doi.org/10.1103/PhysRevD.98.064031
Tolish, A., Bieri, L., Garfinkle, D., & Wald, R. M. (2016). Examination of a simple example of gravitational wave memory. Physical Review D, 90(4), 044060. https://doi.org/10.1103/PhysRevD.90.044060
van Haasteren, R., & Levin, Y. (2010). Gravitational-wave memory and pulsar timing arrays. Monthly Notices of the Royal Astronomical Society, 401(4), 2372-2378. https://doi.org/10.1111/j.1365-2966.2009.15885.x
Wiseman, A. G., & Will, C. M. (1991). Christodoulou's nonlinear gravitational-wave memory: Evaluation in the quadrupole approximation. Physical Review D, 44(10), R2945-R2949. https://doi.org/10.1103/PhysRevD.44.R2945
Zel'dovich, Y. B., & Polnarev, A. G. (1974). Radiation of gravitational waves by a cluster of superdense stars. Soviet Astronomy, 18, 17-21.
Reviews
How to Cite This Review
Replace bracketed placeholders with the reviewer's name (or "Anonymous") and the review date.
