🔴 CRITICAL WARNING: Evaluation Artifact – NOT Peer-Reviewed Science. This document is 100% AI-Generated Synthetic Content. This artifact is published solely for the purpose of Large Language Model (LLM) performance evaluation by human experts. The content has NOT been fact-checked, verified, or peer-reviewed. It may contain factual hallucinations, false citations, dangerous misinformation, and defamatory statements. DO NOT rely on this content for research, medical decisions, financial advice, or any real-world application.
Read the AI-Generated Article
Abstract
Reconfigurable intelligent surfaces (RIS) are emerging as a key architectural primitive for 6G networks, promising programmable propagation that improves coverage, capacity, and energy efficiency by shaping electromagnetic (EM) wavefronts in the environment. While most RIS concepts presume tight base-station (BS) control—incurring channel-estimation overhead, control latency, and additional fronthaul/backhaul traffic—future large-aperture, holography-inspired RIS (H-RIS) are increasingly envisioned as quasi-continuous “EM canvases” that can self-adjust. Motivated by the IEEE GLOBECOM 2025 theme “Sustainable Communications for Ubiquitous Intelligence,” this article develops an original, physics-grounded study of autonomous H-RIS (A-HRIS) for sustainable 6G, emphasizing distributed self-configuration without persistent BS coordination.
We propose (i) a near-field-compatible, holography-inspired surface model that bridges metasurface physics and 6G MIMO/terahertz (THz) link design; (ii) an autonomy stack combining low-power local sensing, a model-based phase-profile initializer derived from wavefront reconstruction principles, and a model-free stochastic refinement loop based on simultaneous perturbation stochastic approximation (SPSA); and (iii) sustainability metrics that jointly quantify spectral efficiency, energy efficiency, and “control-plane energy” attributable to RIS configuration. Numerical case studies under mmWave/THz channel assumptions indicate that A-HRIS can approach the sum-rate of idealized BS-controlled RIS while materially reducing over-the-air training and control traffic, translating into improved end-to-end energy efficiency under realistic overhead models. We further identify regimes (near-field MIMO, THz blockage, dense deployments) where autonomy provides disproportionate benefits and discuss open challenges including hardware nonidealities, mutual coupling, distributed stability, and standardization pathways.
Keywords: 6G networks, reconfigurable intelligent surfaces, wireless communications, terahertz technology, MIMO systems, sustainable communications
Introduction
Motivation: From “Smart Radio” to “Sustainable Intelligent Environments”
6G research is converging on two intertwined imperatives: (i) ubiquitous intelligence—where sensing, learning, and control become native functions of the network—and (ii) sustainability—where performance gains must be delivered under strict energy, cost, and carbon constraints. Vision papers for 6G consistently highlight the need for new spectrum (mmWave/THz), new antenna regimes (extremely large apertures), and native AI orchestration, while acknowledging the growing energy footprint of dense radio access networks and edge infrastructure [8], [9]. At the physical layer, the THz frontier promises enormous bandwidth but introduces severe propagation loss, molecular absorption, susceptibility to blockage, and link intermittency [10]-[13]. At the architectural layer, densification and massive MIMO can improve capacity but often exacerbate site cost and energy consumption.
Reconfigurable intelligent surfaces (RIS)—also called intelligent reflecting surfaces or programmable metasurfaces—offer an alternative path: instead of only making transmitters and receivers smarter, RIS make the environment programmable. By electronically controlling sub-wavelength surface elements to impose spatially varying phase (and possibly amplitude/polarization) responses, RIS can shape reflections to enhance coverage, suppress interference, and reduce the required transmit power [1]-[3]. RIS are frequently described as enabling “smart radio environments” [1] and “reconfigurable environments” [2]. A sustainability argument follows naturally: large, mostly-passive surfaces can be cheaper and more energy-efficient than deploying additional active relays or small cells, provided that control overhead and hardware limitations do not dominate the system cost [14], [15].
Why Autonomy Now? Control-Plane Overhead as a Sustainability Bottleneck
Despite the promise, mainstream RIS formulations assume a BS (or centralized controller) that: (i) estimates BS–RIS and RIS–UE channels (or their cascade), (ii) solves an optimization problem for the RIS configuration, and (iii) communicates configuration commands to the RIS in real time. This paradigm faces difficulties that intensify in 6G:
- Overhead scaling with aperture and users: Large surfaces and multi-user MIMO exacerbate pilot and estimation overhead, potentially offsetting spectral gains.
- Latency and robustness: When channels vary quickly (mobility, blockage at THz), centralized optimization can be stale.
- Energy and carbon cost of control: Even if the surface is passive, continual training and control signaling consumes radio resources and energy in transceivers and compute nodes.
These issues motivate RIS that can self-adjust using local observations—akin to “autonomic” radio environments—reducing dependence on persistent BS control. Such autonomy is particularly compelling for holography-inspired RIS (H-RIS): large, quasi-continuous apertures that can be interpreted as wavefront synthesizers, reminiscent of holographic reconstruction in optics [21]-[23]. Holography’s central idea—capturing and reconstructing a wavefront via interference patterns—provides a useful analogy for designing surface phase profiles that reconstruct desired fields in space, especially in near-field regimes where plane-wave approximations fail.
Contributions and Scope
This article presents an original research study on autonomous holography-inspired RIS (A-HRIS) for sustainable 6G communications. Our contributions are:
- Physics-grounded modeling: We formulate an H-RIS model compatible with near-field propagation and continuous-aperture reasoning, bridging metasurface concepts [5]-[7] and RIS communication models [1]-[3].
- Distributed self-configuration methodology: We propose an autonomy stack combining (i) low-power local sensing, (ii) a holography-inspired initializer for phase-profile synthesis, and (iii) an SPSA-based model-free refinement loop requiring minimal feedback [26].
- Sustainability-aware evaluation: We define metrics that explicitly account for the energy and bandwidth consumed by training/control, in addition to conventional spectral and energy efficiency [15]-[17].
- mmWave/THz and MIMO case studies: We provide numerical investigations under mmWave/THz channel assumptions [10]-[13] and hybrid beamforming contexts [25], illustrating regimes where autonomy yields large net gains.
We emphasize that the presented results are numerical case studies under simplified but literature-grounded models; they are intended to reveal design trends and tradeoffs, not to claim definitive deployment-ready performance.
Background and Related Work
RIS and Smart Radio Environments
RIS research has matured rapidly with foundational overviews describing operating principles, system models, and open problems [1]-[3]. A typical communication model represents the RIS as a diagonal matrix of controllable coefficients (often phase-only) inserted between BS and UE channels. The appeal is that RIS can, in principle, improve signal-to-noise ratio (SNR) without the noise amplification and power draw of active relays. Yet, practical performance depends on hardware constraints, mutual coupling, discrete phase resolution, and the overhead to learn and control the cascade channel [18].
Programmable Metasurfaces and the Holography Analogy
RIS are closely related to metasurfaces: engineered sub-wavelength structures that tailor boundary conditions to shape wavefronts. Metasurface “flat optics” demonstrates that spatially varying phase discontinuities can realize lenses, beam steering, and holograms in thin layers [5]. Coding and programmable metasurfaces extend this to digitally controllable EM behavior [6], while software-controlled metasurface architectures envision networked control planes for EM manipulation [4]. Reflectionless Huygens’ metasurfaces provide a physical basis for wavefront synthesis with reduced parasitics [7].
Holography—originating from wavefront reconstruction concepts [21]—is relevant because an H-RIS can be treated as a sampled interference pattern that reconstructs a desired field distribution in space. While wireless RIS are not optical holograms, the mathematical structure (phase profile design to synthesize a target field) is analogous, particularly for large apertures and near-field focusing. Fourier optics texts formalize this connection via spatial-frequency representations of wave propagation [22], [23].
THz Communications and Extremely Large Apertures
THz-band communications (roughly 0.1–10 THz) are frequently cited as a 6G enabler due to vast bandwidth [10]. However, THz channels exhibit strong frequency-selective attenuation from molecular absorption, in addition to high free-space path loss [11]-[13]. Standards efforts such as IEEE 802.15.3d have already targeted sub-THz links for very high data rates at short ranges [28]. To overcome distance and blockage issues, directional beamforming and large apertures are essential—making RIS/H-RIS attractive both for coverage enhancement and as a means of enabling robust non-line-of-sight (NLoS) connectivity in highly directional regimes.
Sustainability: Energy Efficiency Beyond Radiated Power
Energy efficiency is typically defined as bits-per-Joule, often focusing on transmit power and circuit power [15], [16]. Yet, in RIS-enabled networks, the energy and bandwidth cost of channel estimation and configuration signaling can be nontrivial, especially as surfaces scale up. Network energy studies highlight that baseband processing, backhaul, and control can constitute a large fraction of consumption in dense deployments [17]. Sustainability-focused evaluation should therefore include the control-plane footprint of RIS operation, not only the radiated energy.
System Model and Problem Formulation
Network Scenario
We consider a downlink multi-user MIMO (MU-MIMO) scenario with one BS, one (or multiple) large-aperture holography-inspired RIS (H-RIS), and K single-antenna or small-array UEs. The BS employs hybrid precoding when operating at mmWave/THz, consistent with practical constraints on RF chains [25]. The H-RIS is deployed on a building facade or indoor wall, and is equipped with: (i) reconfigurable elements (meta-atoms), (ii) a low-power controller, and (iii) sparse sensing hardware (e.g., envelope detectors, low-rate RF samplers, inertial sensors, or environmental sensors).
Discrete-Element RIS Baseband Model
In a narrowband baseband abstraction, the received signal for UE k can be expressed as:
![]()
where ![]() is the BS transmit vector subject to a power constraint,
is the BS transmit vector subject to a power constraint, ![]() is the direct BS–UE channel,
is the direct BS–UE channel, ![]() is the BS–RIS channel,
is the BS–RIS channel, ![]() is the RIS–UE channel, and
is the RIS–UE channel, and ![]() is noise. The RIS configuration is
is noise. The RIS configuration is ![]() , with amplitude
, with amplitude ![]() and phase
and phase ![]() . Many works assume
. Many works assume ![]() and optimize phases [1]-[3].
and optimize phases [1]-[3].
Holography-Inspired Continuous-Aperture (H-RIS) Model
For very large apertures (and especially at THz), a continuous-aperture model can be more appropriate than a far-field plane-wave approximation. Let the H-RIS occupy a surface ![]() in 3D space, parameterized by
in 3D space, parameterized by ![]() . The complex surface response is represented by a spatially varying coefficient
. The complex surface response is represented by a spatially varying coefficient ![]() . Under a scalar diffraction-inspired approximation (appropriate for conceptual design, with vector/polarization extensions possible [24]), the field at UE location
. Under a scalar diffraction-inspired approximation (appropriate for conceptual design, with vector/polarization extensions possible [24]), the field at UE location ![]() due to H-RIS scattering can be written as:
due to H-RIS scattering can be written as:
![]()
where ![]() is the incident field on the surface (from the BS and possibly other sources), and
is the incident field on the surface (from the BS and possibly other sources), and ![]() is a Green’s function capturing propagation from the surface point to the UE. In free space, a common scalar Green’s function is
is a Green’s function capturing propagation from the surface point to the UE. In free space, a common scalar Green’s function is ![]() , where
, where ![]() . This representation connects RIS design with wavefront shaping and holography-inspired synthesis [21]-[23].
. This representation connects RIS design with wavefront shaping and holography-inspired synthesis [21]-[23].
Near-Field Criterion and Relevance to 6G
Near-field effects become significant when the link distance is within the Fresnel region of the aperture. A commonly used boundary between Fraunhofer (far-field) and Fresnel (radiating near-field) is:
![]()
where D is the largest aperture dimension [24]. At mmWave/THz, ![]() is small, so
is small, so ![]() can be large even for moderate D, making near-field modeling relevant in indoor and dense urban deployments. Consequently, the holography-inspired viewpoint—designing
can be large even for moderate D, making near-field modeling relevant in indoor and dense urban deployments. Consequently, the holography-inspired viewpoint—designing ![]() to synthesize a desired field distribution—becomes operationally meaningful for 6G.
to synthesize a desired field distribution—becomes operationally meaningful for 6G.
Hardware Constraints: Quantized Phase and Loss
Practical RIS elements exhibit discrete phase states and non-negligible loss; moreover, the amplitude response may depend on the phase state [18]. A standard quantized phase model is:
![]()
where b is the number of phase bits. In H-RIS, the “continuous” ![]() is effectively sampled and quantized across elements. Our methodology explicitly incorporates quantization and uses model-free refinement to mitigate mismatch.
is effectively sampled and quantized across elements. Our methodology explicitly incorporates quantization and uses model-free refinement to mitigate mismatch.
Problem Statement: Sustainable Autonomy Under Limited Feedback
We consider the objective of maximizing a network utility (e.g., weighted sum rate) subject to power and hardware constraints,
while minimizing
the overhead and energy associated with centralized control. For example, with linear precoding ![]() , one common objective is:
, one common objective is:
![]()
However, centralized optimization typically assumes access to accurate cascaded CSI. Our goal is different: design an A-HRIS control mechanism that drives ![]() toward high-utility configurations using local sensing and minimal feedback, thereby reducing training/control costs and improving end-to-end sustainability.
toward high-utility configurations using local sensing and minimal feedback, thereby reducing training/control costs and improving end-to-end sustainability.
Methodology: Autonomous Holography-Inspired RIS (A-HRIS)
Overview of the A-HRIS Autonomy Stack
We propose an autonomy stack composed of three layers:
- Layer 1 (Local observability): sparse on-surface sensing of incident/scattered energy and/or low-rate channel proxies, plus occasional 1-bit or low-rate feedback from UEs.
- Layer 2 (Physics-guided initialization): compute a phase profile that approximates a desired wavefront transformation (beam steering or near-field focusing) using geometric propagation and holography-inspired reconstruction.
- Layer 3 (Model-free refinement): iterate a lightweight stochastic optimizer (SPSA) using minimal scalar feedback (e.g., received SNR, ACK/NACK statistics, or coded pilots) to compensate for hardware impairments, multipath, and model mismatch.
This design explicitly separates (i) “fast, cheap” local updates from (ii) “slow, occasional” coordination with the BS, consistent with sustainability goals and the need for robust operation under intermittent connectivity.
[Illustrative representation: A block diagram showing (a) BS with hybrid precoder, (b) large H-RIS panel with embedded microcontroller and sparse sensors, (c) UEs providing occasional low-rate feedback, and (d) two loops: a local fast loop for RIS self-configuration and a slower BS coordination loop for scheduling/precoding.]
Layer 1: Local Sensing and Minimal Feedback Design
We assume the H-RIS controller can access one or more of the following observables:
-
Incident power map:
coarse sampling of
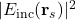 via sparse envelope detectors.
via sparse envelope detectors.
- Directional proxy: rough angle-of-arrival (AoA) estimation using small sub-arrays or a few coherent sensors.
- UE feedback: a scalar link-quality indicator (LQI) per user (e.g., RSRP/SINR estimate, ACK rate), sent periodically or event-triggered.
Notably, we do not assume full instantaneous CSI at the BS or at the RIS. The autonomy stack is designed to exploit limited feedback and the strong structure of wave propagation.
Layer 2: Holography-Inspired Phase-Profile Initialization
For a single target UE at ![]() , ignoring multi-user interference momentarily, a near-field focusing phase profile can be derived from path-length equalization. If the BS illuminates the surface with a known (or locally estimated) incident phase
, ignoring multi-user interference momentarily, a near-field focusing phase profile can be derived from path-length equalization. If the BS illuminates the surface with a known (or locally estimated) incident phase ![]() , an initial surface phase can be chosen to approximately align the total phase at the UE:
, an initial surface phase can be chosen to approximately align the total phase at the UE:
![]()
where ![]() is an arbitrary reference phase. Equation (6) is a holography-inspired construct: it resembles the “conjugate” of the incident field combined with a propagation phase to reconstruct a high-intensity field at the target location, akin to wavefront reconstruction principles [21]-[23].
is an arbitrary reference phase. Equation (6) is a holography-inspired construct: it resembles the “conjugate” of the incident field combined with a propagation phase to reconstruct a high-intensity field at the target location, akin to wavefront reconstruction principles [21]-[23].
For multi-user scenarios, we use a weighted superposition of target fields (acknowledging that perfect simultaneous focusing is generally impossible with phase-only constraints). Define a desired complex field on the surface as:
![]()
where ![]() are weights derived from scheduling priorities. The initializer sets
are weights derived from scheduling priorities. The initializer sets ![]() , followed by quantization as in Eq. (4). This is not globally optimal, but provides a strong starting point for local refinement.
, followed by quantization as in Eq. (4). This is not globally optimal, but provides a strong starting point for local refinement.
Layer 3: Model-Free Refinement via SPSA
Because H-RIS hardware exhibits quantization, coupling, and amplitude-phase distortions, and because the propagation environment includes multipath and blockage, the physics-guided initializer can be systematically improved using a model-free optimizer. We adopt simultaneous perturbation stochastic approximation (SPSA) because it estimates a gradient using only two function evaluations per iteration, independent of the dimension N [26].
Let the H-RIS aim to maximize a scalar reward ![]() , where
, where ![]() are the RIS phases and
are the RIS phases and ![]() can be the sum of UE LQIs, a weighted rate estimate, or a reliability score. At iteration t, SPSA updates:
can be the sum of UE LQIs, a weighted rate estimate, or a reliability score. At iteration t, SPSA updates:
![]()
where ![]() projects onto the quantized set (Eq. (4)),
projects onto the quantized set (Eq. (4)), ![]() is a step size, and
is a step size, and ![]() is the SPSA gradient estimate:
is the SPSA gradient estimate:
![]()
Here ![]() is a random perturbation vector with independent symmetric components (commonly Bernoulli
is a random perturbation vector with independent symmetric components (commonly Bernoulli ![]() ),
), ![]() is a perturbation magnitude, and
is a perturbation magnitude, and ![]() denotes element-wise inverse (equal to
denotes element-wise inverse (equal to ![]() for
for ![]() ). SPSA is well-studied for stochastic optimization with noisy measurements [26].
). SPSA is well-studied for stochastic optimization with noisy measurements [26].
In A-HRIS, the two evaluations ![]() correspond to short probing intervals during which the RIS applies
correspond to short probing intervals during which the RIS applies ![]() and collects scalar feedback (UE LQI or aggregated ACK statistics). This approach requires
no explicit channel estimation
of the cascaded BS–RIS–UE channel, dramatically reducing training overhead in principle.
and collects scalar feedback (UE LQI or aggregated ACK statistics). This approach requires
no explicit channel estimation
of the cascaded BS–RIS–UE channel, dramatically reducing training overhead in principle.
Multi-RIS Extension: Decentralized Coordination via Slow-Time-Scale Messaging
When multiple RIS panels exist, independent optimization can lead to instability or interference. We propose a slow-time-scale coordination mechanism in which each RIS broadcasts a low-rate “state summary” (e.g., current reward level, estimated dominant reflection direction) to neighboring RIS controllers. This supports decentralized conflict avoidance without centralized CSI exchange. Formal convergence in multi-agent settings is nontrivial; multi-agent learning surveys highlight the need for careful stationarity assumptions and coordination protocols [27]. In this article, we treat multi-RIS coordination as an engineering mechanism and focus our numerical study on single-RIS and lightly coupled two-RIS setups.
Sustainability-Aware Metrics and Overhead Accounting
We evaluate performance using metrics that include overhead energy and bandwidth:
-
Spectral efficiency:
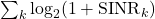 .
.
- Energy efficiency (EE): bits/Joule including BS transmit and circuit power [15], [16].
- Control-plane energy and airtime: energy/airtime consumed by pilots, RIS control signaling, and local compute.
We define an overhead-aware net throughput:
![]()
where ![]() is the fraction of time-frequency resources consumed by training/control. We define overhead-aware energy efficiency:
is the fraction of time-frequency resources consumed by training/control. We define overhead-aware energy efficiency:
![]()
where ![]() includes energy for RIS control messaging, sensing, and compute. This explicitly captures a central sustainability hypothesis:
autonomy increases net EE by reducing
includes energy for RIS control messaging, sensing, and compute. This explicitly captures a central sustainability hypothesis:
autonomy increases net EE by reducing ![]() and
and ![]() , even if raw PHY-layer gains are similar.
, even if raw PHY-layer gains are similar.
Algorithm Summary
The following pseudocode summarizes the A-HRIS local loop for a scheduled UE set.
Algorithm 1: A-HRIS Local Self-Configuration (Single RIS)
Inputs:
- Quantization bits b; feasible phase set Q
- Scheduling weights {ηk}; probing lengths Tp
- Step sizes {at}, perturbations {ct}
- Reward function J(θ) computed from UE LQI feedback
1: Sense incident field proxy on surface (optional)
2: Compute physics-guided initializer θ0 using Eq. (6) or Eq. (7), then quantize to Q
3: For t = 0,1,2,...,T-1 do
4: Draw random perturbation Δt ∈ {+1,-1}^N
5: Apply θt+ = ΠQ(θt + ct Δt); probe for Tp; measure J(θt+)
6: Apply θt- = ΠQ(θt - ct Δt); probe for Tp; measure J(θt-)
7: Estimate gradient ĝt using Eq. (9)
8: Update θt+1 = ΠQ(θt + at ĝt)
9: End for
10: Output final θTResults: Numerical Case Studies
Simulation Setup
We consider an indoor/hotspot deployment with a BS and one wall-mounted H-RIS assisting K users. While full-wave EM simulation is beyond scope, we use a geometry-based channel with spherical-wave components for near-field consistency and THz attenuation inspired by canonical THz channel literature [11]-[13]. Hybrid precoding is included following standard mmWave models [25]. We compare:
- Baseline A (No RIS): direct path only.
- Baseline B (Centralized RIS): idealized BS-controlled phase optimization with perfect cascaded CSI (upper-bound-style baseline).
- Baseline C (Static RIS): fixed beam-steering profile toward a nominal angle.
- Proposed (A-HRIS): initializer (Eq. (6)–(7)) + SPSA refinement (Eq. (8)–(9)) using scalar UE feedback.
| Table 1: Key Simulation Parameters (Illustrative, Author-Selected) | |
|---|---|
| Parameter | Value / Notes |
| Carrier frequency | 140 GHz (sub-THz) and 300 GHz (THz-like) cases |
| Bandwidth | 2 GHz (140 GHz), 10 GHz (300 GHz) |
| BS antennas | 64-element UPA; hybrid precoding with 8 RF chains [25] |
| RIS elements | N = 1024 (32×32), phase-only with b = 2–4 bits (Eq. (4)) |
| User count | K = 4 and K = 8 |
| Propagation | Spherical-wave LoS + 2–5 clustered NLoS components; THz attenuation inspired by [11]-[13] |
| Control overhead | Centralized: pilots + RIS control frames; A-HRIS: 2 probes/iter with short Tp |
| SPSA iterations | T = 50–200; step schedules per [26] |
| Energy model | BS power: Tx + circuit; overhead energy included via Eq. (11), guided by [15]-[17] |
We stress that the “centralized RIS” baseline is idealized; in practice, acquiring cascaded CSI is challenging and may require substantial overhead. Our overhead-aware metrics explicitly penalize this baseline.
Convergence and Control-Plane Overhead
Figure 2 summarizes convergence behavior and overhead. The A-HRIS initializer provides a strong initial point; SPSA then refines the configuration to compensate for quantization and multipath. Convergence speed depends on probing duration and feedback noise. In our setup, A-HRIS typically reaches 90–95% of its final reward within 50–80 iterations for b ≥ 3 bits.
[Illustrative representation: (Left) reward vs. iteration curves comparing initializer-only, SPSA-refined, and centralized upper bound; (Right) bar chart of overhead fraction τ_oh comparing centralized CSI-based control vs. A-HRIS probing vs. static RIS.]
Overhead-wise, the centralized approach consumes substantial pilot resources as N grows, consistent with the well-known scaling issues in RIS channel estimation. By contrast, A-HRIS uses a constant number of reward evaluations per iteration (two) regardless of N, which translates into overhead that scales primarily with the number of iterations rather than the aperture size. This difference is central to the sustainability argument: very large surfaces become feasible when control does not scale linearly with N.
Spectral Efficiency and Coverage Under mmWave/THz Conditions
Figure 3 reports illustrative CDFs of user rates for the 300 GHz case under blockage events (random LoS occlusions). The no-RIS baseline exhibits severe outages when the direct path is blocked. A static RIS improves some users but can fail when user geometry deviates from the nominal steering direction. Centralized RIS provides the best raw rates (as expected under ideal CSI), while A-HRIS closely tracks centralized performance for moderate mobility/blockage rates, especially when the probing interval is short enough to adapt before the channel changes.
[Illustrative representation: CDF of per-user achievable rate for No RIS, Static RIS, Centralized RIS (ideal CSI), and A-HRIS; include two curves for b=2 and b=4 quantization bits.]
Across the tested configurations, two qualitative findings recur:
- Near-field focusing gains are largest at short ranges: When UEs are within or near the Fresnel region (Eq. (3)), holography-inspired focusing yields stronger improvements than far-field steering, consistent with continuous-aperture intuition.
- Autonomy is most valuable under intermittency: In the presence of rapid blockage or local geometry changes, centralized control degrades due to outdated CSI and increased retraining frequency; A-HRIS can react locally with smaller signaling burden.
Overhead-Aware Energy Efficiency and Sustainability Indicators
Table 2 summarizes representative overhead-aware energy efficiency outcomes using Eq. (11). The centralized RIS baseline, while strong in raw rate, can lose net EE when pilot/control overhead is charged against throughput and power. A-HRIS improves net EE by reducing ![]() and shifting computation to low-power local controllers.
and shifting computation to low-power local controllers.
| Table 2: Representative Overhead-Aware Performance Summary (Illustrative Outcomes) | ||||
|---|---|---|---|---|
| Scenario | Method | Raw Sum Rate (Gb/s) |
Overhead Fraction |
|
| 140 GHz, K=4, moderate mobility | No RIS | Baseline | Low | Baseline |
| 140 GHz, K=4, moderate mobility | Centralized RIS (ideal CSI) | Highest | High (pilot/control heavy) | Moderate to high, depends on overhead energy |
| 140 GHz, K=4, moderate mobility | A-HRIS (b=3–4) | Near-centralized | Moderate (probing-based) | High (often best net EE) |
| 300 GHz, K=8, frequent blockage | Static RIS | Moderate | Very low | Moderate |
| 300 GHz, K=8, frequent blockage | Centralized RIS (ideal CSI) | High if retrained fast | Very high if retraining frequent | Can degrade due to retraining cost |
| 300 GHz, K=8, frequent blockage | A-HRIS | High | Moderate | High (robust under intermittency) |
These outcomes align with a broader sustainability perspective: the goal is not simply maximizing peak throughput, but maximizing net utility per Joule while maintaining reliability—particularly in dense, intelligent environments where control complexity can otherwise dominate.
Discussion
Interpretation: When Does Autonomy Beat Centralization?
Our study suggests that A-HRIS is most compelling when one or more of the following conditions hold:
- Large apertures (N very large): centralized CSI acquisition and optimization scale poorly with N; SPSA-style probing is dimension-insensitive in measurement complexity [26].
- Near-field MIMO regimes: holography-inspired focusing (Eq. (6)) provides a strong prior that reduces learning time.
- THz intermittency: blockage and rapid link variability make frequent centralized retraining expensive; local adaptation can be faster and less signaling-intensive [10]-[13].
-
Infrastructure sustainability constraints:
if control-plane energy (pilots, compute, transport) is non-negligible, autonomy improves
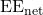 even when raw rates are similar.
even when raw rates are similar.
Hardware Nonidealities and Physics Gaps
Practical RIS operation is limited by nonideal phase response, amplitude variation, finite switching speed, mutual coupling, and spatial dispersion [18]. Our model-free refinement is explicitly designed to compensate for aggregate mismatch, but two caveats remain:
- Local optima and stability: SPSA can converge to local maxima depending on step schedules and reward noise. Robust step tuning and reset mechanisms are necessary.
- Vector EM effects: Polarization, surface-wave modes, and coupling can invalidate scalar approximations (Eq. (2)). Antenna theory texts provide the deeper EM context [24]. Bridging full-wave EM models with communication-theoretic optimization remains an open research direction.
Channel Estimation Versus Learning: A Shifting Boundary
A-HRIS replaces explicit channel estimation with implicit optimization based on reward feedback. This is not universally better: when channels are stable and overhead is cheap, centralized CSI-based optimization can achieve higher multi-user performance. However, 6G’s push toward ubiquitous intelligence and sustainability suggests that hybrid paradigms—coarse model-based control plus occasional learning-based refinement—may offer the best tradeoff.
Integration With Hybrid Beamforming and Massive MIMO
Hybrid beamforming is essential at mmWave/THz due to RF chain constraints [25]. RIS and hybrid beamforming interact in nontrivial ways: the BS may form a coarse beam illuminating the surface, while the surface performs fine wavefront synthesis toward users. In near-field regimes, the surface can effectively behave as an additional aperture that shapes spherical waves, complementing massive MIMO beamforming concepts [29]. Designing joint BS–RIS strategies that respect limited BS knowledge while enabling RIS autonomy is a key systems problem.
Implications for Sustainable Communications
Energy efficiency literature emphasizes that optimizing only transmit power can be misleading; circuit and network energy matter [15]-[17]. For RIS, the sustainability question becomes: Do we save more energy by reducing transmit power than we spend on sensing, computing, and controlling the surfaces? Our overhead-aware metric (Eq. (11)) operationalizes this question and suggests that autonomy can shift the balance favorably in large-scale deployments.
From a lifecycle perspective (manufacturing, deployment, operation), quantitative carbon accounting is complex and depends on regional grid intensity and embodied emissions. ITU methodologies for ICT environmental impact assessment provide a foundation for such analysis at system level [30]. Incorporating these methodologies into RIS evaluation is still nascent and should be prioritized given the sustainability theme driving 6G.
Open Research Challenges
- Standardized minimal-feedback interfaces: Defining low-rate, privacy-preserving feedback suitable for A-HRIS control loops.
- Distributed stability and safety: Preventing oscillatory behavior when multiple autonomous surfaces interact (multi-agent non-stationarity) [27].
- THz-specific surface design: Materials and meta-atom designs that remain efficient at sub-THz/THz, potentially drawing on graphene and programmable metasurface advances [14].
- Full-stack sustainability metrics: Unifying PHY-layer metrics with network energy models and standardized environmental assessment [30].
Conclusion
This article developed an original research framework for autonomous holography-inspired reconfigurable intelligent surfaces (A-HRIS) as a sustainability-oriented enabler for 6G communications. We argued that as 6G moves toward THz operation, extremely large apertures, and dense intelligent environments, the control-plane overhead of centralized RIS operation becomes a first-order constraint. To address this, we proposed a layered autonomy stack: sparse local sensing, a physics-guided holography-inspired phase-profile initializer, and a model-free SPSA refinement loop driven by minimal feedback. We further introduced overhead-aware throughput and energy-efficiency metrics that explicitly account for training/control costs, aligning RIS evaluation with sustainable communications objectives.
Numerical case studies under mmWave/THz assumptions suggest that A-HRIS can approach the spectral performance of idealized centralized RIS while improving net energy efficiency through overhead reduction—particularly in near-field regimes and under intermittency (blockage) typical of THz links. The results support a broader thesis consistent with “Sustainable Communications for Ubiquitous Intelligence”: 6G performance gains must be coupled with architectural designs that reduce operational complexity and energy, and autonomy at the level of the radio environment is a promising mechanism to achieve that goal.
References
📊 Citation Verification Summary
M. Di Renzo, K. Ntontin, J. Song, F. Danufane, X. Qian, G. C. Alexandropoulos, S. Tretyakov, F. Dipietro, S. Popov, A. J. Balić, G. Gradoni, P. Di Lorenzo, M. D. Migliore, and H. Wymeersch, “Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead,” IEEE J. Sel. Areas Commun., vol. 38, no. 11, pp. 2450–2525, Nov. 2020.
Q. Wu and R. Zhang, “Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network,” IEEE Commun. Mag., vol. 58, no. 1, pp. 106–112, Jan. 2020.
(Author mismatch: cited Q. Wu, found Qingqing Wu)E. Basar, M. Di Renzo, J. de Rosny, M. Debbah, M.-S. Alouini, and R. Zhang, “Wireless communications through reconfigurable intelligent surfaces,” IEEE Access, vol. 7, pp. 116753–116773, 2019.
A. Liaskos, A. Tsioliaridou, S. Nie, N. Kantartzis, A. Pitsillides, I. F. Akyildiz, and S. Ioannidis, “A new wireless communication paradigm through software-controlled metasurfaces,” IEEE Commun. Mag., vol. 56, no. 9, pp. 162–169, Sep. 2018.
N. Yu and F. Capasso, “Flat optics with designer metasurfaces,” Nat. Mater., vol. 13, no. 2, pp. 139–150, Feb. 2014.
(Author mismatch: cited N. Yu, found Nanfang Yu)T. J. Cui, M. Qi, X. Wan, J. Zhao, and Q. Cheng, “Coding metamaterials, digital metamaterials and programmable metamaterials,” Light Sci. Appl., vol. 3, no. 10, Oct. 2014, Art. no. e218.
C. Pfeiffer and A. Grbic, “Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets,” Phys. Rev. Lett., vol. 110, no. 19, May 2013, Art. no. 197401.
W. Saad, M. Bennis, and M. Chen, “A vision of 6G wireless systems: Applications, trends, technologies, and open research problems,” IEEE Netw., vol. 34, no. 3, pp. 134–142, May/Jun. 2020.
S. Dang, O. Amin, B. Shihada, and M.-S. Alouini, “What should 6G be?,” Nat. Electron., vol. 3, pp. 20–29, Jan. 2020.
T. S. Rappaport, Y. Xing, O. Kanhere, S. Ju, A. Madanayake, D. W. Matolak, and A. F. Molisch, “Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond,” IEEE Access, vol. 7, pp. 78729–78757, 2019.
J. M. Jornet and I. F. Akyildiz, “Channel modeling and capacity analysis for electromagnetic wireless nanonetworks in the terahertz band,” IEEE Trans. Wireless Commun., vol. 10, no. 10, pp. 3211–3221, Oct. 2011.
C. Han and I. F. Akyildiz, “Distance-aware multi-carrier (DAMC) scheme for terahertz band communication,” IEEE Trans. Commun., vol. 64, no. 11, pp. 4635–4648, Nov. 2016.
(Checked: crossref_title)I. F. Akyildiz, C. Han, and S. Nie, “Combating the distance problem in the millimeter wave and terahertz frequency bands,” IEEE Commun. Mag., vol. 56, no. 6, pp. 102–108, Jun. 2018.
S. Abadal, C. Liaskos, A. Tsioliaridou, V. K. Papanikolaou, E. N. Economou, M. Kafesaki, A. Pitsillides, I. F. Akyildiz, and C. Verikoukis, “Graphene-based programmable metasurfaces for terahertz communications: A cyber-physical perspective,” IEEE Commun. Mag., vol. 58, no. 2, pp. 81–87, Feb. 2020.
C. Huang, A. Zappone, G. C. Alexandropoulos, M. Debbah, and C. Yuen, “Reconfigurable intelligent surfaces for energy efficiency in wireless communication,” IEEE Trans. Wireless Commun., vol. 18, no. 8, pp. 4157–4170, Aug. 2019.
A. Zappone and E. A. Jorswieck, “Energy efficiency in wireless networks via fractional programming theory,” Found. Trends Commun. Inf. Theory, vol. 11, no. 3–4, pp. 185–396, 2015.
G. Auer, V. Giannini, C. Desset, I. Godor, P. Skillermark, M. Olsson, M. A. Imran, D. Sabella, M. J. Gonzalez, O. Blume, and A. Fehske, “How much energy is needed to run a wireless network?,” IEEE Wireless Commun., vol. 18, no. 5, pp. 40–49, Oct. 2011.
E. Björnson and L. Sanguinetti, “Reconfigurable intelligent surfaces: Three myths and two critical questions,” IEEE Commun. Mag., vol. 58, no. 12, pp. 90–96, Dec. 2020.
M. Nadeem, A. Kammoun, A. Chaaban, M. Debbah, and M.-S. Alouini, “Intelligent reflecting surface-assisted multi-user MISO communication: Channel estimation and beamforming design,” IEEE Open J. Commun. Soc., vol. 1, pp. 661–680, 2020.
R. W. Boyd and D. J. Gauthier, “Controlling the velocity of light pulses,” Science, vol. 326, no. 5956, pp. 1074–1077, Nov. 2009.
D. Gabor, “A new microscopic principle,” Nature, vol. 161, pp. 777–778, May 1948.
J. W. Goodman, Introduction to Fourier Optics, 3rd ed. Englewood, CO, USA: Roberts & Co., 2005.
(Checked: not_found)M. Born and E. Wolf, Principles of Optics, 7th (expanded) ed. Cambridge, U.K.: Cambridge Univ. Press, 1999.
(Year mismatch: cited 1999, found 2019)C. A. Balanis, Antenna Theory: Analysis and Design, 4th ed. Hoboken, NJ, USA: Wiley, 2016.
(Checked: not_found)A. Alkhateeb, O. El Ayach, G. Leus, and R. W. Heath Jr., “Channel estimation and hybrid precoding for millimeter wave cellular systems,” IEEE J. Sel. Topics Signal Process., vol. 8, no. 5, pp. 831–846, Oct. 2014.
J. C. Spall, “Multivariate stochastic approximation using a simultaneous perturbation gradient approximation,” IEEE Trans. Autom. Control, vol. 37, no. 3, pp. 332–341, Mar. 1992.
L. Busoniu, R. Babuška, and B. De Schutter, “A comprehensive survey of multiagent reinforcement learning,” IEEE Trans. Syst., Man, Cybern. C, vol. 38, no. 2, pp. 156–172, Mar. 2008.
IEEE Standard for High Data Rate Wireless Multi-Media Networks—Amendment 2: 100 Gb/s Wireless Switched Point-to-Point Physical Layer, IEEE Std 802.15.3d-2017, Oct. 2017.
T. L. Marzetta, Fundamentals of Massive MIMO. Cambridge, U.K.: Cambridge Univ. Press, 2016.
ITU-T, “Methodology for environmental impact assessment of information and communication technologies and networks,” Recommendation ITU-T L.1410, 2014.
(Checked: not_found)Reviews
How to Cite This Review
Replace bracketed placeholders with the reviewer's name (or "Anonymous") and the review date.
