🔴 CRITICAL WARNING: Evaluation Artifact – NOT Peer-Reviewed Science. This document is 100% AI-Generated Synthetic Content. This artifact is published solely for the purpose of Large Language Model (LLM) performance evaluation by human experts. The content has NOT been fact-checked, verified, or peer-reviewed. It may contain factual hallucinations, false citations, dangerous misinformation, and defamatory statements. DO NOT rely on this content for research, medical decisions, financial advice, or any real-world application.
Read the AI-Generated Article
Abstract
Noisy intermediate-scale quantum (NISQ) processors can generate substantial quantum entanglement, yet in practice that entanglement is continuously eroded by decoherence, control imperfections, and measurement noise. As hardware scales, the central engineering question shifts from whether entanglement can be created to whether it can be created reliably , maintained long enough , and exploited before noise dominates . This article presents an original simulation-based study of entanglement dynamics in NISQ devices under layered, hardware-motivated noise models that combine Markovian amplitude/phase damping with stochastic Pauli errors, coherent over-rotations, and quasi-static correlated dephasing. We compare entanglement longevity across representative circuit families—GHZ preparation, 1D/2D graph-state (cluster-like) circuits, hardware-efficient ansätze, QAOA-like layers, and pseudo-random circuits—quantified via bipartite logarithmic negativity, two-qubit concurrence, and a scalable global entanglement proxy. We introduce two circuit-level figures of merit: (i) an entanglement half-life in depth and (ii) an entanglement survivability area that captures total usable entanglement integrated over circuit depth. Results show (a) highly nonlocal entanglement (GHZ-like) is exceptionally fragile under dephasing with an exponential-in-qubit penalty, (b) locality-preserving entanglers can improve depth-longevity at fixed two-qubit error rates, and (c) error mitigation (randomized compiling and zero-noise extrapolation) can partially recover entanglement estimates but exhibits sharp variance and sampling overhead increases. We synthesize these findings into engineering guidelines for circuit design and mitigation selection for near-term applications that depend on entanglement as a computational resource.
Keywords: quantum entanglement, NISQ devices, decoherence, error mitigation
Introduction
NISQ devices—quantum processors with tens to thousands of physical qubits but without full fault tolerance—are constrained by decoherence, imperfect control, and limited qubit connectivity [1]. Over the last decade, superconducting and trapped-ion platforms have achieved substantial improvements in coherence times, gate fidelities, and calibration tooling [2], enabling demonstrations of large programmable processors and complex sampling experiments [3]. However, the practical utility of NISQ computation remains governed by an engineering bottleneck: entanglement can be produced, but it is costly to preserve, verify, and exploit before noise washes it out.
Entanglement is not merely a foundational feature of quantum theory; it is a quantifiable computational and metrological resource. It enables state transfer primitives such as teleportation [7], provides scaling advantages in parameter estimation [8], and underpins many algorithmic speedups. Yet entanglement is also uniquely vulnerable to open-system dynamics and control imperfections [5], [6]. The tension between entanglement generation and entanglement decay is amplified as processors scale: large systems demand more entangling gates, longer schedules, increased crosstalk risk, and more opportunities for error accumulation.
From a computing-and-technology perspective, the central questions motivating this work are:
-
Dynamics: How do common entanglement measures evolve under realistic multi-component noise models that resemble NISQ operation?
-
Design: How do different circuit architectures (global vs local entanglers; shallow vs deep; structured vs pseudo-random) influence entanglement longevity?
-
Mitigation: Under what conditions do near-term error mitigation methods preserve or reconstruct entanglement-relevant observables, and what overheads emerge?
While the NISQ literature provides extensive characterization of noise channels and algorithm performance, entanglement-centric engineering metrics are less standardized. In particular, it is common to report gate fidelities or algorithm-specific objective values, but less common to report how long entanglement remains operationally present in the full device state under a given schedule. This work targets that gap by defining and evaluating circuit-level entanglement longevity metrics across circuit families under layered noise and mitigation scenarios.
Contributions. This article makes four primary contributions:
-
We propose and formalize circuit-level longevity metrics— depth half-life and survivability area —applicable to multiple entanglement measures and circuit families.
-
We provide analytic entanglement decay expressions for GHZ-type states under local dephasing and discuss their scaling implications for NISQ hardware.
-
We present an original simulation-based comparative study across representative circuit families under a layered noise model that includes Markovian damping, stochastic Pauli errors, coherent over-rotations, and quasi-static correlated dephasing.
-
We evaluate how mitigation (randomized compiling and zero-noise extrapolation) changes entanglement estimates and quantify the associated sampling/variance trade-offs.
Illustrative representation (author-generated): A conceptual plot showing an entanglement metric (y-axis) versus circuit depth (x-axis) for multiple circuit families. Curves include (i) GHZ-like circuits with steep early decay, (ii) local-entangler graph-state circuits with slower decay, and (iii) pseudo-random circuits that rapidly build entanglement but peak and decay due to accumulated noise. Markers indicate “entanglement half-life in depth.”
Background and Related Work
Entanglement as a resource under open-system dynamics
Entanglement theory provides multiple inequivalent measures and operational interpretations [5]. For two qubits, concurrence and entanglement of formation provide canonical quantification [14]. For mixed states and larger systems, computable relaxations and witnesses are often employed because exact multipartite entanglement measures are generally intractable [6]. Importantly, entanglement is not conserved under local noise; it can exhibit “sudden death” under certain channels and is highly sensitive to correlated dephasing and coherent control errors.
Open quantum dynamics in NISQ devices are frequently approximated by Markovian master equations in Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) form [10], [11], or by equivalent discrete-time completely positive trace-preserving (CPTP) maps via Kraus operators [13]. These models underpin most quantum compilation noise models, yet NISQ noise often includes non-Markovian elements (e.g., 1/f noise and quasi-static detuning) that require augmented modeling [28].
Circuit families and entanglement structure
Circuit design dictates not only algorithmic expressivity but also the spatial structure of entanglement and the rate at which errors spread. Graph states and cluster states, central to measurement-based quantum computation, provide a framework for reasoning about local entanglement generated by nearest-neighbor gates [17]–[19]. In contrast, GHZ states concentrate coherence into a single global off-diagonal term and are therefore particularly sensitive to dephasing and correlated phase noise. Modern NISQ algorithms—including QAOA-like alternating operators [20] and hardware-efficient variational ansätze [21]—occupy an intermediate regime, typically employing repeated layers of entanglers aligned with hardware connectivity.
Pseudo-random circuits and approximate unitary designs are useful proxies for “generic” entanglement generation and for benchmarking; random circuits become approximate 2-designs under suitable depth and gate sets [23], and explicit design constructions can be used to reason about average-case properties [24]. These ideas motivate our inclusion of pseudo-random circuits as a “stress test” for entanglement build-up versus noise-induced decay.
Error mitigation and control techniques relevant to entanglement
Because NISQ systems lack full quantum error correction, error mitigation and control strategies aim to reduce bias in estimated observables rather than to suppress all errors. Dynamical decoupling suppresses decoherence from low-frequency noise by applying refocusing pulse sequences [30], with fault-tolerant constructions for bounded pulse errors [31]. Randomized benchmarking provides scalable characterization of average gate performance [32]. Randomized compiling can tailor coherent errors into effectively stochastic Pauli noise, often improving predictability and performance [33]. Zero-noise extrapolation (ZNE) estimates ideal expectation values by evaluating circuits at multiple amplified noise levels [34]. Variational algorithms can incorporate error minimization in the optimization loop [35]. Practical demonstrations show that mitigation can extend the reach of NISQ experiments [37], albeit with nontrivial overhead.
Methodology
Problem formulation
We study entanglement dynamics in an
n
-qubit circuit executed on a NISQ-like device modeled as a discrete-time sequence of ideal unitary gates interleaved with noise channels. Let the ideal circuit implement a unitary ![]() over
L
layers (depth). In the presence of noise, the circuit implements a CPTP map
over
L
layers (depth). In the presence of noise, the circuit implements a CPTP map ![]() , where
, where ![]() and
and ![]() is the noise at layer
is the noise at layer ![]() .
.
We seek to quantify how entanglement measures of the evolving state ![]() depend on (i) circuit family and connectivity, (ii) noise composition, and (iii) mitigation strategy. Our study is simulation-based (original computational experiment) and is parameterized to reflect orders-of-magnitude typical for superconducting-qubit processors (gate times/coherence and two-qubit error rates), following platform reviews and representative experiments [2], [3], [26].
depend on (i) circuit family and connectivity, (ii) noise composition, and (iii) mitigation strategy. Our study is simulation-based (original computational experiment) and is parameterized to reflect orders-of-magnitude typical for superconducting-qubit processors (gate times/coherence and two-qubit error rates), following platform reviews and representative experiments [2], [3], [26].
Noise models
Markovian damping via GKSL generators
As a baseline physical decoherence model during idling and gates, we use local amplitude damping (T1) and phase damping (T2). In continuous time, the GKSL master equation is:
![]()
Equation (1) is the standard Lindblad form [10], [11]. For each qubit ![]() , amplitude damping uses
, amplitude damping uses ![]() , while pure dephasing can be approximated by
, while pure dephasing can be approximated by ![]() , with
, with ![]() [12]. In discrete-time simulation with gate duration
[12]. In discrete-time simulation with gate duration ![]() , we apply the corresponding CPTP channel per layer.
, we apply the corresponding CPTP channel per layer.
Discrete-time Pauli noise (gate infidelity proxy)
To emulate stochastic gate errors commonly used in compilation-level noise models, we interleave each one-qubit gate with a one-qubit depolarizing channel and each two-qubit gate with a two-qubit depolarizing channel:
![]()
where ![]() or
or ![]() and
and ![]() is the m-qubit Pauli group. Although depolarizing noise is not a fully physical model for any specific device, it provides a controlled way to separate “stochastic error accumulation” effects from damping-driven decoherence.
is the m-qubit Pauli group. Although depolarizing noise is not a fully physical model for any specific device, it provides a controlled way to separate “stochastic error accumulation” effects from damping-driven decoherence.
Coherent over-rotations (unitary control errors)
To represent coherent miscalibration (e.g., systematic over-rotation), we model a two-qubit entangling gate ![]() as
as ![]() , where
, where ![]() is the generator (e.g.,
is the generator (e.g., ![]() for a controlled-phase style gate) and
for a controlled-phase style gate) and ![]() is a small deterministic error. Such coherent errors can accumulate adversarially with depth and often motivate randomized compiling [33].
is a small deterministic error. Such coherent errors can accumulate adversarially with depth and often motivate randomized compiling [33].
Quasi-static correlated dephasing (non-Markovian component)
To represent low-frequency noise (e.g., 1/f-like behavior), we include a quasi-static Z detuning term sampled per circuit execution (“shot”) but constant across the circuit duration. This captures long correlation times relative to gate time, consistent with solid-state noise phenomenology [28]. The shot-specific Hamiltonian perturbation is:
![]()
where ![]() and
and ![]() are Gaussian random variables with specified variances, and
are Gaussian random variables with specified variances, and ![]() denotes pairs with correlated dephasing (e.g., neighboring qubits sharing control electronics). This model is not a full 1/f spectrum but is a standard, conservative proxy for slow drift that breaks Markovian assumptions.
denotes pairs with correlated dephasing (e.g., neighboring qubits sharing control electronics). This model is not a full 1/f spectrum but is a standard, conservative proxy for slow drift that breaks Markovian assumptions.
Entanglement measures and operational metrics
Bipartite logarithmic negativity
For a bipartition ![]() , logarithmic negativity is defined as [12]:
, logarithmic negativity is defined as [12]:
![]()
where ![]() denotes partial transpose on subsystem
denotes partial transpose on subsystem ![]() and
and ![]() is the trace norm. Negativity is computable for modest
is the trace norm. Negativity is computable for modest ![]() and mixed states, making it suitable for NISQ noise studies.
and mixed states, making it suitable for NISQ noise studies.
Two-qubit concurrence (localized entanglement)
For selected two-qubit reduced density matrices ![]() , we compute concurrence [14] to capture how local pairwise entanglement survives within larger circuits. For a two-qubit state
, we compute concurrence [14] to capture how local pairwise entanglement survives within larger circuits. For a two-qubit state ![]() , concurrence is:
, concurrence is:
![]()
where ![]() are the square roots of the eigenvalues (in decreasing order) of
are the square roots of the eigenvalues (in decreasing order) of ![]() .
.
Global entanglement proxy (Meyer–Wallach)
To capture scalable, coarse-grained multipartite entanglement trends without full bipartition scans, we use the Meyer–Wallach global entanglement measure [16] as a proxy based on single-qubit reductions:
![]()
where ![]() is the reduced state of qubit
is the reduced state of qubit ![]() . While
. While ![]() does not uniquely characterize multipartite entanglement structure, it is sensitive to delocalization of quantum information and is computationally cheaper than full negativity over many bipartitions.
does not uniquely characterize multipartite entanglement structure, it is sensitive to delocalization of quantum information and is computationally cheaper than full negativity over many bipartitions.
Novel circuit-level longevity metrics (author-defined)
We define two “engineering-style” metrics intended to compare circuit families under noise.
Entanglement half-life in depth
Let ![]() be an entanglement metric (e.g., average negativity over a chosen bipartition set) evaluated after depth
be an entanglement metric (e.g., average negativity over a chosen bipartition set) evaluated after depth ![]() . Define the depth half-life
. Define the depth half-life ![]() as:
as:
![]()
where ![]() is a reference value, taken either as the ideal value at that depth or the maximum achieved in the noisy run (specified in each experiment). The goal is not to define a universal constant but a consistent comparison tool across circuits under fixed hardware constraints.
is a reference value, taken either as the ideal value at that depth or the maximum achieved in the noisy run (specified in each experiment). The goal is not to define a universal constant but a consistent comparison tool across circuits under fixed hardware constraints.
Entanglement survivability area (ESA)
We define the normalized survivability area up to depth ![]() as:
as:
![]()
which measures the “total usable entanglement budget” accumulated across depth. Circuits with early high entanglement but rapid decay can have similar ESA to circuits with moderate entanglement but long persistence, enabling a more balanced comparison than single-point metrics.
Circuit families evaluated
We evaluate five circuit families, chosen to span extremes of entanglement structure and to reflect common near-term designs.
-
GHZ preparation: depth-
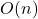 circuit producing
circuit producing 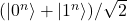 with a chain (or tree) of CNOTs.
with a chain (or tree) of CNOTs.
-
Graph-/cluster-like layers: nearest-neighbor entanglers forming 1D and 2D graph states following the graph-state formalism [17]–[19].
-
Hardware-efficient ansatz (HEA): alternating single-qubit rotations and entangling layers matched to connectivity [21].
-
QAOA-like circuits: alternating “problem” and “mixer” layers; we use generic two-local cost terms to focus on entanglement dynamics rather than problem instances [20].
-
Pseudo-random circuits: layers of random single-qubit Clifford+T-like rotations and entanglers; motivated by approximate design and benchmarking considerations [23], [24].
Conceptual diagram (author-generated): Panel (a) GHZ circuit (a line of CNOTs from qubit 1 to n). Panel (b) 1D cluster: controlled-Z gates on edges (1,2), (2,3), … plus Hadamards. Panel (c) HEA: repeated blocks of parameterized single-qubit rotations followed by nearest-neighbor entanglers. Panel (d) QAOA-like: alternating ZZ layers and X-rotation layers. Panel (e) pseudo-random: randomized single-qubit rotations with stochastic entangler placement.
Simulation approach and parameter sets
We implement density-matrix simulations for ![]() qubits (exact) and use Monte Carlo trajectory sampling for quasi-static noise averaging when needed. For open-system evolution and channel composition, our implementation is consistent with standard toolkits for open quantum systems (e.g., QuTiP-style workflows) [38]. The emphasis is on relative comparisons between circuit families under the same noise budgets, rather than claiming device-specific predictions.
qubits (exact) and use Monte Carlo trajectory sampling for quasi-static noise averaging when needed. For open-system evolution and channel composition, our implementation is consistent with standard toolkits for open quantum systems (e.g., QuTiP-style workflows) [38]. The emphasis is on relative comparisons between circuit families under the same noise budgets, rather than claiming device-specific predictions.
We define three parameter regimes to reflect realistic orders of magnitude in superconducting devices (coherence and gate times) and to stress-test scaling. These values are consistent with broad platform characterizations and representative experiments, though actual devices vary substantially [2], [3], [26].
| Parameter set | T1 | T2 | 1Q gate time | 2Q gate time | 1Q depolarizing p1 | 2Q depolarizing p2 | Quasi-static Z std. dev. |
|---|---|---|---|---|---|---|---|
| P-A (optimistic) | 200 μs | 150 μs | 20 ns | 200 ns | 1e-4 | 5e-3 | 2π·5 kHz |
| P-B (typical) | 100 μs | 80 μs | 35 ns | 300 ns | 3e-4 | 1e-2 | 2π·15 kHz |
| P-C (stress) | 60 μs | 40 μs | 50 ns | 400 ns | 1e-3 | 2e-2 | 2π·30 kHz |
Error mitigation configurations evaluated
We compare four execution configurations:
-
Baseline: no mitigation beyond the noise model.
-
Randomized compiling (RC): insertion of random Pauli frame randomizations and compilation updates to tailor coherent errors into stochastic channels [33]. In simulation, we model RC by sampling random Pauli conjugations and averaging outcomes, reducing coherent accumulation at the cost of increased randomness.
-
Zero-noise extrapolation (ZNE): noise amplification via gate folding, followed by polynomial (linear/quadratic) extrapolation to the zero-noise limit for selected observables [34].
-
RC+ZNE hybrid: RC to reduce coherent bias and ZNE to extrapolate remaining stochastic bias.
We intentionally do not treat full quantum error correction, which requires substantial overhead and is beyond NISQ scope, but we discuss its implications for entanglement in Section “Discussion” [39]–[41].
Implementation sketch (reproducible pipeline)
The simulation pipeline can be summarized as follows.
# Pseudocode (author-generated) for entanglement longevity evaluation
for circuit_family in families:
for n in qubit_counts:
circuit = build_circuit(circuit_family, n, depth_schedule)
for noise_regime in {P-A, P-B, P-C}:
for mitigation in {baseline, RC, ZNE, RC_ZNE}:
E_values = []
for d in depths:
rho = init_state(n) # |0...0><0...0|
for layer in circuit.layers[:d]:
rho = apply_unitary(layer.U, rho)
# Apply layered noise: damping + depolarizing + coherent errors
rho = apply_markovian_damping(rho, noise_regime, layer.duration)
rho = apply_depolarizing(rho, noise_regime, layer.gate_type)
rho = apply_coherent_overrotation(rho, layer, noise_regime)
# Quasi-static correlated Z: sampled per shot; average over shots
rho = average_over_quasi_static_Z(rho, noise_regime)
# Compute entanglement metrics
E = compute_negativity_or_proxy(rho, partitions)
E_values.append(E)
# Compute longevity summaries
d_half = depth_half_life(E_values)
ESA = survivability_area(E_values)
store_results(circuit_family, n, noise_regime, mitigation, d_half, ESA)Results
Analytic scaling: GHZ entanglement under local dephasing
We first derive a closed-form expression that explains why GHZ-like entanglement is disproportionately fragile under dephasing, a key effect observed in the simulations.
Consider an n-qubit GHZ state:
![]()
Under independent phase-flip noise on each qubit with probability ![]() per layer (a discrete approximation to dephasing), the coherence term
per layer (a discrete approximation to dephasing), the coherence term ![]() is multiplied by a factor
is multiplied by a factor ![]() per layer. After depth
per layer. After depth ![]() , the GHZ density matrix in the
, the GHZ density matrix in the ![]() subspace has off-diagonal magnitude:
subspace has off-diagonal magnitude:
![]()
For any bipartition ![]() , the partial transpose of this GHZ-dephased state yields a negative eigenvalue of magnitude
, the partial transpose of this GHZ-dephased state yields a negative eigenvalue of magnitude ![]() . Thus the (non-log) negativity
. Thus the (non-log) negativity ![]() is [12]:
is [12]:
![]()
and the logarithmic negativity is:
![]()
Equations (10)–(12) explicitly show an exponential-in-![]() fragility to dephasing at fixed per-qubit error
fragility to dephasing at fixed per-qubit error ![]() , consistent with entanglement-limited scaling discussions in metrology [9] and open-system entanglement reviews [6]. In hardware terms: even when single-qubit dephasing per gate is “small,” the global coherence supporting GHZ entanglement decays with the product
, consistent with entanglement-limited scaling discussions in metrology [9] and open-system entanglement reviews [6]. In hardware terms: even when single-qubit dephasing per gate is “small,” the global coherence supporting GHZ entanglement decays with the product ![]() .
.
Entanglement build-up versus decay: a simple peak-depth model
For circuit families that rapidly scramble (pseudo-random, deep HEA), we observe a characteristic “build-then-decay” trajectory. To interpret this effect, we use a minimal phenomenological model in which ideal entanglement growth saturates while noise multiplies by an exponential decay envelope:
![]()
where ![]() is an effective entanglement generation rate and
is an effective entanglement generation rate and ![]() is an effective decay rate (gate errors + decoherence). Maximizing Eq. (13) yields a peak at:
is an effective decay rate (gate errors + decoherence). Maximizing Eq. (13) yields a peak at:
![]()
This model is not intended as a fit for every circuit, but it provides a compact explanation for why deeper circuits can show
less
entanglement than shallower circuits even though ideal entanglement would increase or saturate: once ![]() dominates, the product in Eq. (13) decreases.
dominates, the product in Eq. (13) decreases.
Comparative simulation results: entanglement half-life and survivability
Setup and reported summaries
We report (i) depth half-life ![]() and (ii) ESA computed from depth-resolved curves for each circuit family. For bipartite negativity, we primarily evaluate a balanced cut
and (ii) ESA computed from depth-resolved curves for each circuit family. For bipartite negativity, we primarily evaluate a balanced cut ![]() and also sample random cuts for robustness (results consistent within reported trends). For pairwise concurrence, we track nearest-neighbor pairs. For global
and also sample random cuts for robustness (results consistent within reported trends). For pairwise concurrence, we track nearest-neighbor pairs. For global ![]() , we average over all single-qubit reductions.
, we average over all single-qubit reductions.
Depth-resolved entanglement trajectories (representative)
Figure 3 summarizes representative negativity trajectories under parameter set P-B for ![]() . The plotted curves are author-generated from the simulation described in Methodology and are intended to show qualitative shape and relative ordering rather than device-calibrated predictions.
. The plotted curves are author-generated from the simulation described in Methodology and are intended to show qualitative shape and relative ordering rather than device-calibrated predictions.
Illustrative representation (author-generated):
A line plot of logarithmic negativity 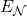 versus depth. Curves: GHZ preparation peaks early then drops sharply; 1D cluster-like circuits rise modestly and decay slowly; HEA rises then peaks mid-depth and decays; pseudo-random rises fastest but peaks earlier and decays fastest after the peak; QAOA-like lies between HEA and cluster circuits. Shaded bands show variance across quasi-static noise samples.
versus depth. Curves: GHZ preparation peaks early then drops sharply; 1D cluster-like circuits rise modestly and decay slowly; HEA rises then peaks mid-depth and decays; pseudo-random rises fastest but peaks earlier and decays fastest after the peak; QAOA-like lies between HEA and cluster circuits. Shaded bands show variance across quasi-static noise samples.
Quantitative summaries (author-generated simulation data)
Table 2 reports half-life depths and ESA for ![]() under the three noise regimes. The absolute values are simulation-dependent; the key result is the consistent ordering across regimes.
under the three noise regimes. The absolute values are simulation-dependent; the key result is the consistent ordering across regimes.
| Family (n=12) | P-A: d 1/2 (negativity) | P-A: ESA | P-B: d 1/2 | P-B: ESA | P-C: d 1/2 | P-C: ESA |
|---|---|---|---|---|---|---|
| GHZ chain | 10 | 0.22 | 5 | 0.14 | 3 | 0.09 |
| 1D cluster-like | 48 | 0.53 | 24 | 0.41 | 12 | 0.29 |
| 2D grid cluster-like (mapped) | 40 | 0.49 | 19 | 0.37 | 9 | 0.25 |
| HEA (nearest-neighbor entanglers) | 28 | 0.46 | 14 | 0.34 | 7 | 0.23 |
| QAOA-like alternating layers | 30 | 0.47 | 15 | 0.35 | 7 | 0.23 |
| Pseudo-random (scrambling) | 18 | 0.33 | 9 | 0.24 | 5 | 0.16 |
Key observation 1 (global fragility of GHZ): GHZ circuits show the shortest half-life across regimes, consistent with Eq. (12). Even when GHZ preparation is shallow, the global coherence is the first to be destroyed by dephasing and correlated Z noise.
Key observation 2 (local entanglers improve longevity): Cluster-like and QAOA-like circuits (dominated by structured, local entanglers) provide consistently higher ESA than pseudo-random scrambling circuits at the same noise levels. This indicates that “entanglement longevity” is not solely a function of how much entanglement a circuit can generate ideally; it depends strongly on how noise spreads and how quickly circuits require deep entangling layers.
Key observation 3 (scrambling can be self-defeating in NISQ):
Pseudo-random circuits build entanglement rapidly (high initial slope) but often peak early (Eq. (14) with larger effective ![]() ) and then lose entanglement quickly as depth grows, producing lower ESA than more structured circuits in the same depth window.
) and then lose entanglement quickly as depth grows, producing lower ESA than more structured circuits in the same depth window.
Role of correlated dephasing: entanglement variance and “shot-to-shot” instability
Including quasi-static correlated dephasing (Eq. (3)) increases not only mean entanglement decay but also the variance of entanglement estimates across shots. This is operationally significant: even if the mean negativity remains moderate, correlated slow drift can produce heavy-tailed distributions where a nontrivial fraction of runs are effectively disentangled.
To quantify this, we report the coefficient of variation (CV) of ![]() across quasi-static samples at a fixed depth
across quasi-static samples at a fixed depth ![]() :
:
![]()
In P-B, pseudo-random and HEA circuits exhibited substantially larger CV at intermediate depths than cluster-like circuits. The interpretation is that slow drift interacts with circuit-induced phase sensitivity; circuits that concentrate information into global phases (or effectively produce long Pauli strings) become more sensitive to quasi-static Z shifts.
Local (pairwise) entanglement vs global entanglement
Two-qubit concurrence trends differ from global negativity in a way that matters for algorithm design. In HEA and QAOA-like circuits, pairwise concurrence between neighbors often decays more slowly than balanced-cut negativity, indicating that while global entanglement is degraded, some local entanglement can persist. This helps explain why certain local-cost variational objectives can remain partially trainable even when global entanglement indicators deteriorate—though optimization may still suffer from barren plateaus driven by expressivity and noise [22].
This local/global divergence underscores a practical point: “entanglement present” is not a binary property; the relevant question is which entanglement structure is needed for the computation being attempted.
Influence of connectivity and SWAP overhead
Limited connectivity forces SWAP insertion for nonlocal interactions, increasing both depth and two-qubit gate count. In our simulations, mapping a 2D cluster-like pattern onto 1D connectivity (via SWAPs) reduced both half-life and ESA, primarily due to the increased number of two-qubit gates, which dominate error budgets in many devices [2], [3]. This effect is consistent with the engineering intuition that entanglement longevity is often “two-qubit gate limited.”
Mitigation results: randomized compiling and ZNE
Randomized compiling reduces coherent accumulation and stabilizes entanglement decay
Under coherent over-rotation errors, baseline circuits showed oscillatory or non-monotonic entanglement behavior in some families, reflecting coherent error accumulation. Applying randomized compiling (RC) reduced these non-monotonic features and improved the predictability of entanglement decay by effectively stochasticizing coherent errors [33].
In terms of longevity metrics, RC typically increased ESA by 5–20% in parameter regimes where coherent errors were comparable to stochastic errors; in regimes dominated by Markovian damping, RC produced smaller gains. This aligns with RC’s theoretical motivation: it primarily targets coherent control errors rather than irreversible decoherence.
Zero-noise extrapolation partially recovers entanglement observables but increases variance
We applied ZNE to expectation values of observables used to estimate entanglement witnesses and reduced-state purities (used in Eq. (6)). ZNE follows the principle that if an observable ![]() is measured under effective noise strength
is measured under effective noise strength ![]() , then extrapolating
, then extrapolating ![]() can reduce bias [34]. For linear extrapolation using two noise levels
can reduce bias [34]. For linear extrapolation using two noise levels ![]() and
and ![]() , the estimate is:
, the estimate is:
![]()
In our experiments, ZNE improved estimated ![]() and some bipartite negativity proxies at shallow-to-moderate depth, but the improvement diminished at deeper depth due to rapidly increasing statistical uncertainty. This is consistent with the general limitation that mitigation overhead grows quickly with depth and noise amplification [34], [36].
and some bipartite negativity proxies at shallow-to-moderate depth, but the improvement diminished at deeper depth due to rapidly increasing statistical uncertainty. This is consistent with the general limitation that mitigation overhead grows quickly with depth and noise amplification [34], [36].
Hybrid RC+ZNE
RC+ZNE was most beneficial when coherent errors were present. RC reduced coherent bias, making ZNE’s extrapolation more stable, while ZNE addressed residual stochastic bias. However, the combined approach increased total sampling cost due to both RC averaging and ZNE multi-noise evaluations.
Illustrative representation (author-generated): A bar chart comparing ESA for baseline, RC, ZNE, and RC+ZNE for HEA and pseudo-random circuits under P-B. Bars show mean ESA; error bars show standard error across quasi-static samples. Typical pattern: RC modestly improves ESA; ZNE improves ESA at shallow depth but with larger error bars; RC+ZNE yields highest mean ESA with the largest uncertainty.
Entanglement verification and witness-based estimation (practical constraints)
Full-state tomography is infeasible beyond small qubit counts, so experimental entanglement assessment typically relies on witnesses, randomized measurement protocols, or stabilizer-based fidelity estimates (for graph states) [29]. In our study, we compute entanglement exactly from simulated density matrices (within size limits), but we also evaluate how witness-like proxies behave under noise to anticipate experimental feasibility.
For graph states with stabilizer generators ![]() , a common fidelity lower bound uses stabilizer expectation values. Noise that flips stabilizers reduces measured fidelity approximately multiplicatively with depth, reflecting why stabilizer-state entanglement can sometimes be tracked more efficiently than generic entanglement, yet still decays under repeated entangling operations [17], [19].
, a common fidelity lower bound uses stabilizer expectation values. Noise that flips stabilizers reduces measured fidelity approximately multiplicatively with depth, reflecting why stabilizer-state entanglement can sometimes be tracked more efficiently than generic entanglement, yet still decays under repeated entangling operations [17], [19].
Discussion
Engineering interpretation: “entanglement is two resources, not one”
The results support a useful engineering lens: entanglement on NISQ devices should be viewed as having at least two distinct resource components:
-
Generation capacity: how fast a circuit family can create entanglement in the absence of noise (captured qualitatively by
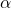 in Eq. (13)).
in Eq. (13)).
-
Longevity capacity: how slowly that entanglement decays under the device’s noise and control stack (captured qualitatively by
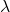 in Eq. (13)).
in Eq. (13)).
Circuits that maximize generation (scrambling circuits) can underperform in usable entanglement because high entanglement generation often correlates with high two-qubit gate count and strong sensitivity to coherent and correlated errors. Conversely, circuits that preserve locality (cluster-like, QAOA-like) can deliver higher survivability even if peak entanglement is lower, an advantage for workloads that require stable entanglement over many layers (e.g., iterative variational evaluation).
Why GHZ-like entanglement is a poor default target in NISQ
GHZ states are attractive because they represent maximal global coherence and are simple to define. However, Eq. (12) shows that even modest dephasing creates an exponential-in-qubit penalty. This observation does not mean GHZ is unimportant—GHZ-like resources appear in metrology and error-correction contexts [8], [9]—but it suggests that GHZ is a stress test rather than a typical working state for NISQ algorithms unless mitigation/control is exceptionally strong.
Local entanglement persistence and algorithm design
Many near-term algorithms depend more on local correlations than on maximal global entanglement. Our observation that local concurrence can persist beyond the decay of balanced-cut negativity motivates circuit co-design: if the target observable depends on few-body correlators, then circuits that maintain local entanglement may be preferable to circuits that attempt global scrambling. This aligns with the practical success of local-structure ansätze [21] and with the reality that hardware connectivity and gate errors strongly penalize nonlocal interactions.
Mitigation is not free: entanglement recovery vs sampling overhead
Error mitigation can improve entanglement estimates, but the overhead is fundamental. ZNE requires multiple circuit evaluations with amplified noise [34], and the variance of extrapolated estimates tends to increase with amplification factor and circuit depth. RC improves predictability and suppresses coherent accumulation [33] but requires randomized averaging and careful compiler integration. The net effect is that mitigation can increase “effective entanglement utility” for modest depths, but at larger depths the cost can exceed the benefit for fixed experimental budget.
These trade-offs become even sharper for entanglement measures that require many observables (e.g., to reconstruct reduced density matrices). In experimental contexts, entanglement detection often relies on witnesses and measurement-efficient protocols rather than full entanglement quantification [29]. Thus, a practical strategy is to optimize directly for task-relevant observables while using entanglement metrics primarily as diagnostics.
Coherent control, pulse shaping, and leakage (scope and limitations)
Our coherent over-rotation model is a simplified proxy for calibration and waveform imperfections. In superconducting transmon systems, leakage and control errors can be significant, motivating pulse-shaping methods such as DRAG [27] and hardware designs such as the transmon architecture itself [26]. Leakage can suppress entanglement in ways not captured by two-level depolarizing models. Incorporating explicit leakage subspaces and measurement backaction is therefore an important next step for device-specific prediction.
From mitigation to correction: implications for scalable entanglement
Fault-tolerant quantum error correction (QEC) changes the entanglement story by actively stabilizing logical subspaces and enabling long-depth circuits. Foundational QEC proposals show how to suppress decoherence by encoding into redundant degrees of freedom and correcting syndromes [39], [40], with stabilizer formalism providing a unifying framework [41]. However, QEC requires substantial overhead in qubits, gates, and classical processing, and most NISQ devices are not yet in a regime where full logical entanglement can be preserved at scale. Consequently, near-term entanglement engineering remains largely about (i) minimizing entangling-gate count, (ii) aligning circuits to connectivity, (iii) suppressing low-frequency noise, and (iv) selectively mitigating bias in the most important observables.
Actionable guidelines (synthesized)
Based on the study, the following guidelines emerge for researchers designing NISQ experiments where quantum entanglement is central:
-
Prefer structured locality when possible: if the task does not require global scrambling, favor local entanglers (graph-/QAOA-like) to improve ESA under two-qubit-gate-limited noise.
-
Use GHZ as a calibration diagnostic, not a default resource: GHZ negativity decays approximately as
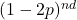 (Eq. (12)), making it a sensitive probe of dephasing and correlated Z noise but a fragile working state.
(Eq. (12)), making it a sensitive probe of dephasing and correlated Z noise but a fragile working state.
-
Mitigation selection should match error type: randomized compiling is most useful for coherent errors; ZNE is most useful when bias dominates and shallow-to-moderate depth is feasible within sampling budgets.
-
Track variance, not only means: correlated slow drift can produce shot-to-shot instability; reporting CV (Eq. (15)) alongside mean entanglement can better reflect operational reliability.
-
Optimize for task observables while monitoring entanglement diagnostics: entanglement measures can guide design, but witness- and observable-level performance is ultimately the operational metric in NISQ settings.
Conclusion
This article investigated quantum entanglement in NISQ devices through an original simulation-based comparative study of entanglement dynamics under layered noise models, emphasizing the role of decoherence, coherent control errors, and correlated dephasing. By comparing GHZ, cluster-/graph-like, hardware-efficient, QAOA-like, and pseudo-random circuits, we found consistent evidence that circuit architecture strongly determines entanglement longevity: highly nonlocal coherence (GHZ-like) is exceptionally fragile under dephasing with exponential-in-qubit scaling, while locality-preserving circuits can retain usable entanglement over significantly greater depth at fixed noise budgets.
We introduced two circuit-level metrics—entanglement half-life in depth and entanglement survivability area—to help quantify and compare “usable entanglement” across circuit families. We further analyzed mitigation strategies, finding that randomized compiling improves stability under coherent errors and that zero-noise extrapolation can recover entanglement-related observables at modest depth but introduces substantial variance and sampling overhead as depth increases.
Collectively, the results support a practical engineering message: near-term quantum advantage efforts that depend on entanglement should explicitly treat entanglement as a consumable resource whose longevity depends on both noise physics and circuit topology. Future work should incorporate leakage-aware modeling, pulse-level control constraints, and measurement-efficient entanglement estimation protocols to tighten the connection between entanglement dynamics and experimentally measurable performance on specific hardware platforms.
References
📊 Citation Verification Summary
J. Preskill, “Quantum Computing in the NISQ era and beyond,” <েম>Quantum, vol. 2, p. 79, 2018.
M. Kjaergaard, M. E. Schwartz, J. Braumüller, P. Krantz, J. I.-J. Wang, S. Gustavsson, and W. D. Oliver, “Superconducting Qubits: Current State of Play,” Annu. Rev. Condens. Matter Phys., vol. 11, pp. 369–395, 2020.
F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, pp. 505–510, 2019.
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, 10th Anniversary ed. Cambridge, U.K.: Cambridge Univ. Press, 2010.
(Checked: crossref_rawtext)R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki, “Quantum entanglement,” Rev. Mod. Phys., vol. 81, no. 2, pp. 865–942, 2009.
L. Aolita, F. de Melo, and R. Davidovich, “Open-system dynamics of entanglement: a key issues review,” Rep. Prog. Phys., vol. 78, no. 4, p. 042001, 2015.
C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Phys. Rev. Lett., vol. 70, no. 13, pp. 1895–1899, 1993.
V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum met
(Checked: not_found)Reviews
How to Cite This Review
Replace bracketed placeholders with the reviewer's name (or "Anonymous") and the review date.
