Comparative Analysis of Settling Velocity Formulations for Natural Sediment Particles: From Stokes (1851) to Contemporary Models

Review Article

REF: CIV-2912

Comparing Settling Velocities of Sediment Particles

The settling velocity of a particle can be determined by balancing the net downward gravitational force with the opposing drag force as it moves through a fluid. However, when applied to sediment particles with irregular shapes and surfaces, the resulting equations are typically empirical and accurate only for the specific datasets or conditions on which they were developed. In this review, we examine the available settling velocities reported in the literature, from Stokes (1851) to studies in 2025, highlighting their differences, strengths, and limitations, and propose a method to compare them systematically in a tabular format.

REVIEWS

[2] Total

[0] Meets Standards

[0] Needs Work

[2] Below Standards

VERIFICATION

[—]% Plagiarism

[—]% AI-Generated

via Originality.ai

83.2% Cite-Ref Score

MODEL

GPT-5.1

Temperature: 0.45

Max Tokens: 15000

Suggested by Amin Riazi

⚑ Flag This Paper ✎ Offer a Review

🔴 CRITICAL WARNING: Evaluation Artifact – NOT Peer-Reviewed Science. This document is 100% AI-Generated Synthetic Content. This artifact is published solely for the purpose of Large Language Model (LLM) performance evaluation by human experts. The content has NOT been fact-checked, verified, or peer-reviewed. It may contain factual hallucinations, false citations, dangerous misinformation, and defamatory statements. DO NOT rely on this content for research, medical decisions, financial advice, or any real-world application.

Read the AI-Generated Article

Abstract

The settling velocity of sediment particles underpins a wide range of processes in hydraulic engineering, morphodynamics, and environmental modeling. Classical theory determines the settling velocity by balancing the net downward gravitational force with the opposing drag force as a particle moves through a fluid. For natural sediment particles, however, irregular shapes, surface roughness, and particle–fluid interactions render purely theoretical approaches inadequate, and most available formulations are semi-empirical or fully empirical, calibrated against specific datasets. This review synthesizes key developments in settling velocity research from Stokes (1851) to studies published up to 2025, with emphasis on sediment particles in water. We summarize foundational theoretical work, widely used empirical and semi-empirical equations, and recent data-driven and shape-aware formulations. A systematic tabular framework is proposed for comparing settling velocity equations based on: (i) underlying drag formulation, (ii) particle shape and roughness representation, (iii) Reynolds number and size ranges, (iv) sediment and fluid properties, and (v) validation datasets and error metrics. The review highlights strengths and limitations of major approaches, identifies persistent gaps in representing irregular natural grains, and suggests a standardized methodology for benchmarking existing and future settling velocity models. This framework is intended to support more transparent model selection and facilitate the development of generalized, transferable formulations for engineering and environmental applications.

Introduction

Settling velocity is a fundamental parameter in sediment transport, water and wastewater treatment, estuarine and coastal morphodynamics, and aquatic ecology. It governs the residence time of particles in the water column, influences bedload and suspended load partitioning, and affects contaminant transport when pollutants are sorbed onto sediment particles (van Rijn, 1993; Soulsby, 1997). For an isolated rigid particle in a quiescent, Newtonian fluid, the terminal settling velocity arises from the balance between the net downward gravitational force and the upward drag force. In its simplest form, this balance yields analytical expressions for spherical particles at low Reynolds numbers, most notably Stokes’ law (Stokes, 1851).

Natural sediment particles, however, deviate significantly from the idealized smooth sphere. They exhibit irregular shapes, angularity, variable surface roughness, and often occur as aggregates or flocs. These features modify the drag coefficient and, consequently, the settling velocity (Dietrich, 1982; Ferguson & Church, 2004). Moreover, the hydrodynamic regime spans several orders of magnitude in Reynolds number, from laminar to fully turbulent, and may involve hindered settling at higher concentrations, cohesive effects, and biological binding in fine-grained sediments (Winterwerp, 2002; Mehta, 2014). As a result, most practical settling velocity formulations for sediment particles are empirical or semi-empirical, calibrated against laboratory or field data under specific conditions.

The proliferation of such formulations poses a challenge for researchers and practitioners: different equations often yield substantially different settling velocities for the same particle size and density, leading to uncertainty in sediment transport predictions. Furthermore, many equations are valid only within narrow ranges of particle size, density ratio, or Reynolds number, and their applicability to other conditions is unclear. While several reviews have addressed aspects of drag on irregular particles or settling of specific sediment types (e.g., Dietrich, 1982; Chien & Wan, 1999; Loth, 2008; Tran-Cong et al., 2004), there is a need for a systematic, comparative framework that spans the historical development from Stokes (1851) to contemporary models and explicitly targets natural sediment particles.

This article has three main objectives:

To review the theoretical foundations of settling velocity and drag, and summarize key empirical and semi-empirical formulations used for sediment particles.
To synthesize the differences, strengths, and limitations of these formulations across particle sizes, shapes, and flow regimes.
To propose a systematic, tabular methodology for comparing settling velocity equations, enabling transparent benchmarking and informed model selection.

The focus is on non-cohesive and weakly cohesive sediment particles in water, with attention to how drag force parameterizations and shape descriptors are incorporated. The review is intended for researchers in hydraulic engineering, sedimentology, and environmental fluid mechanics who require robust and transparent tools for predicting settling velocity.

Literature Review

Fundamental force balance and Stokes’ law

The terminal settling velocity $w_s$ of a single particle in a quiescent fluid is obtained by balancing forces in the vertical direction. For a particle of volume $V_p$ , projected area $A_p$ , density $\rho_s$ , in a fluid of density $\rho_f$ and dynamic viscosity $\mu$ , the force balance at terminal velocity is

$(\rho_s - \rho_f) V_p g = \tfrac{1}{2} C_D \rho_f A_p w_s^2, \tag{1}$

where $g$ is gravitational acceleration and $C_D$ is the drag coefficient. For a smooth sphere of diameter $d$ at low Reynolds number $Re = \rho_f w_s d / \mu \ll 1$ , Stokes (1851) derived an analytical expression for the drag force, yielding

$w_s = \frac{(\rho_s - \rho_f) g d^2}{18 \mu}. \tag{2}$

Equation (2) is widely known as Stokes’ law and is valid for isolated, rigid, smooth spheres in creeping flow. It provides a rigorous theoretical baseline and is still used in fine-sediment applications where $Re \lesssim 1$ . However, most natural sand and gravel particles settle at higher Reynolds numbers, where inertial effects become important and $C_D$ departs from the Stokes regime.

Drag coefficient correlations for spheres

To extend beyond the Stokes regime, numerous correlations have been developed for the drag coefficient of spheres as a function of Reynolds number. A commonly used composite expression is due to Schiller and Naumann (1933):

$C_D = \frac{24}{Re} \left(1 + 0.15 Re^{0.687}\right), \quad Re \leq 800. \tag{3}$

For higher Reynolds numbers, $C_D$ approaches an approximately constant value (e.g., $C_D \approx 0.44$ for smooth spheres in fully turbulent flow). Such correlations, when combined with the force balance in Equation (1), provide implicit or explicit expressions for $w_s$ of spherical particles (Clift, Grace, & Weber, 1978). These formulations are foundational but do not account for the irregular shapes of natural sediment particles.

Shape effects and irregular sediment particles

Irregular particle shape modifies both the projected area $A_p$ and the drag coefficient $C_D$ . Early work introduced simple shape factors, such as sphericity $\psi$ , defined as the ratio of the surface area of a volume-equivalent sphere to the actual particle surface area (Wadell, 1933). Subsequent studies have used Corey shape factor, flatness and elongation ratios, and other descriptors (Corey, 1949; Zingg, 1935).

Dietrich (1982) provided one of the most influential empirical formulations for the settling velocity of natural sand and gravel, explicitly incorporating shape and roundness. He compiled an extensive dataset of settling velocities for natural particles in water and proposed a dimensionless settling velocity $W^*$ related to a dimensionless particle diameter $D_*$ , with corrections for particle shape and roundness. Although the full expression is complex, the general structure can be summarized as

$W^* = f(D_*, S, R), \tag{4}$

where $S$ is a shape parameter and $R$ is roundness. Dietrich’s (1982) work demonstrated that particle shape can significantly reduce settling velocity relative to an equivalent sphere, especially for platy or elongated grains.

Subsequent studies have proposed alternative shape-aware drag correlations. Tran-Cong, Gay, and Michaelides (2004) developed a drag coefficient formula for non-spherical particles based on equivalent diameter and sphericity, validated against numerical simulations and experiments. Loth (2008) reviewed drag models for non-spherical particles and highlighted the importance of orientation and particle Reynolds number. These works, while not limited to sediment, provide a theoretical and empirical basis for shape effects relevant to natural grains.

Widely used empirical and semi-empirical settling velocity formulas for sediments

Rubey (1933)

Rubey (1933) derived an expression for the settling velocity of sediment particles by combining Stokes’ law at low Reynolds numbers with a turbulent drag regime at high Reynolds numbers. For a spherical particle of diameter $d$ , Rubey’s formula can be written as

$w_s = \sqrt{\frac{4 (\rho_s - \rho_f) g d}{3 C_D \rho_f}}, \tag{5}$

with $C_D$ expressed as a function of $Re$ . In practice, Rubey’s formulation is often implemented in iterative form or approximated by piecewise expressions. It has been widely used in early sediment transport modeling but assumes spherical particles.

Soulsby (1997)

Soulsby (1997) proposed a compact empirical formula that smoothly transitions between viscous and turbulent regimes for sand-sized particles in seawater. In one commonly used form, the settling velocity is approximated as

$w_s = \frac{\nu}{d} \left( \sqrt{10.36^2 + 1.049 D_*^3} - 10.36 \right), \tag{6}$

where $\nu$ is kinematic viscosity and $D_*$ is a dimensionless grain size defined by

$D_* = d \left[ \frac{(\rho_s / \rho_f - 1) g}{\nu^2} \right]^{1/3}. \tag{7}$

Soulsby’s formulation is convenient and widely adopted in coastal and estuarine models. It implicitly assumes spherical or near-spherical quartz sand and is calibrated for typical marine conditions, limiting its direct applicability to highly irregular or very fine/coarse sediments.

Ferguson and Church (2004)

Ferguson and Church (2004) introduced a semi-empirical formula that is both simple and physically interpretable, applicable across a wide range of particle sizes from fine sand to coarse gravel. Their expression for settling velocity is

$w_s = \frac{R g d^2}{C_1 \nu + \sqrt{0.75 C_2 R g d^3}}, \tag{8}$

where $R = (\rho_s / \rho_f - 1)$ is the submerged specific density, $\nu$ is kinematic viscosity, and $C_1$ , $C_2$ are empirical coefficients. For natural quartz sediment in water, Ferguson and Church (2004) recommended $C_1 = 18$ and $C_2 = 1.0$ for spheres, with adjustments for irregular grains. Equation (8) recovers Stokes’ law in the viscous limit and a turbulent drag regime at high Reynolds numbers, offering a continuous transition without iteration.

Other notable formulations

Several other settling velocity equations have been proposed for specific sediment types or size ranges. Chien and Wan (1999) summarized a number of Chinese and international formulas for sediment in rivers, including piecewise expressions for fine, medium, and coarse particles. van Rijn (1993) provided practical formulas for sand and gravel in hydraulic engineering applications, often building on Rubey-type approaches. For cohesive sediments and flocs, Winterwerp (2002) and Mehta (2014) developed models that incorporate floc size distributions, fractal structure, and aggregation–breakup dynamics, recognizing that the effective settling velocity of flocs is time- and shear-dependent.

Hindered settling and concentration effects

At higher sediment concentrations, interactions among particles reduce the effective settling velocity, a phenomenon known as hindered settling. Richardson and Zaki (1954) proposed a widely used empirical relation for the hindered settling velocity $w_h$ relative to the single-particle settling velocity $w_s$ :

$\frac{w_h}{w_s} = (1 - \phi)^n, \tag{9}$

where $\phi$ is the volumetric solids concentration and $n$ is an empirical exponent that depends on Reynolds number and particle properties. While Equation (9) is not specific to sediment, it has been extensively applied in sedimentation and slurry transport. For natural sediments, hindered settling interacts with flocculation, turbulence, and stratification, complicating the direct use of single-particle settling velocity models.

Recent advances: data-driven and high-fidelity approaches

In the last two decades, advances in imaging, particle tracking, and computational fluid dynamics (CFD) have enabled more detailed characterization of drag and settling behavior for irregular particles. Direct numerical simulations (DNS) and lattice Boltzmann methods have been used to compute drag coefficients for realistic grain geometries at various Reynolds numbers (e.g., Yin & Koch, 2007; Tenneti & Subramaniam, 2014). High-resolution 3D scanning and micro-computed tomography (micro-CT) allow precise measurement of particle shape and surface roughness, which can be incorporated into drag models.

Parallel to these developments, machine learning and regression techniques have been applied to large experimental datasets to derive data-driven correlations for drag and settling velocity that account for multiple shape descriptors (e.g., Bagheri & Bonadonna, 2016; Haider & Levenspiel, 1989 for earlier regression-based drag correlations). Although many such studies focus on industrial particles or volcanic ash, the methodologies are directly relevant to sediment particles and suggest pathways toward more generalizable settling velocity models.

Synthesis of Studies

Common theoretical structure

Despite the diversity of formulations, most settling velocity models share a common theoretical structure derived from the force balance in Equation (1). The key differences arise in how the drag coefficient $C_D$ and geometric parameters ( $V_p$ , $A_p$ ) are represented. Conceptually, settling velocity models can be categorized as:

Theoretical–analytical: Derived from first principles under restrictive assumptions (e.g., Stokes’ law for spheres at low $Re$ ).
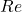Semi-empirical: Combine theoretical limits (laminar and turbulent) with empirical coefficients to ensure smooth transitions (e.g., Ferguson & Church, 2004; Soulsby, 1997).
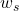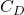Empirical: Direct regression of $w_s$ or $C_D$ against particle and fluid properties, often with limited theoretical underpinning (e.g., some river sediment formulas summarized by Chien & Wan, 1999).
Data-driven / high-fidelity: Use CFD or machine learning to derive drag correlations from detailed simulations or large experimental datasets (e.g., Tran-Cong et al., 2004; Bagheri & Bonadonna, 2016).

Across these categories, the central challenge for sediment particles is to represent the drag force in a way that captures the effects of irregular shape, surface roughness, and orientation, while remaining computationally tractable for engineering applications.

Key dimensions and parameters for comparison

To systematically compare settling velocity formulations, we identify a set of key dimensions and parameters that characterize each model:

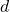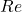Particle size and Reynolds number range: Minimum and maximum $d$ and $Re$ for which the model has been validated.
Particle shape representation: Use of sphericity, Corey shape factor, aspect ratios, or no explicit shape parameter.
Density ratio and fluid properties: Range of 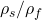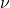$\rho_s / \rho_f$ , $\nu$ , and temperature/salinity conditions.
Drag coefficient formulation: Analytical, empirical, or data-driven 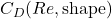$C_D(Re, \text{shape})$ and whether it is implicit or explicit in $w_s$ .
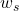Concentration effects: Whether the model addresses hindered settling or assumes isolated particles.
Validation data: Type (laboratory vs. field), sediment type (quartz sand, gravel, cohesive mud, flocs), and sample size.
Error metrics and performance: Reported mean absolute error, bias, or other statistics relative to measured settling velocities.

These dimensions form the basis of the proposed tabular comparison framework in the next subsection.

Proposed tabular framework for systematic comparison

To enable transparent comparison of settling velocity formulations, we propose a standardized table structure with the following columns:

Model ID / Reference (e.g., Stokes, 1851; Dietrich, 1982; Ferguson & Church, 2004).
Equation form (explicit 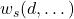$w_s(d, \dots)$ , implicit via 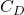$C_D$ , or tabulated).
Particle size range (e.g., $1 \, \mu\text{m} \leq d \leq 1 \, \text{mm}$ ).
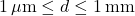Reynolds number range (e.g., $10^{-3} \leq Re \leq 10^4$ ).
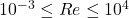Particle shape treatment (sphere, sphericity 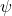$\psi$ , Corey factor, aspect ratios, none).
Density ratio / fluid conditions (e.g., quartz in freshwater at 20°C; seawater; variable).
Drag formulation ( 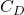$C_D$ correlation, laminar–turbulent blending, CFD-based, etc.).
Concentration regime (isolated particle; includes hindered settling; flocculation effects).
Calibration dataset (number of data points, sediment type, experimental setup).
Reported accuracy (e.g., RMSE, bias, typical error percentage).
Intended application (riverine sand, gravel, cohesive mud, industrial particles).

An example subset of such a table, focusing on widely cited models for non-cohesive sediment, might appear as follows (values indicative, not exhaustive):

Model / Reference	Equation form	Size range	Shape treatment	Drag formulation	Concentration	Calibration data	Reported accuracy	Notes / Intended use
Stokes (1851)	Explicit, Eq. (2)	$d \lesssim 100 \, \mu\text{m}$	Sphere	Analytical laminar	Isolated	Theoretical	Exact for assumptions	Baseline for fine particles, low $Re$
Rubey (1933)	Implicit via $C_D$ , Eq. (5)	Sand–gravel	Sphere	Laminar + turbulent blend	Isolated	Lab data, quartz sand	Within ~10–20% for calibration range	Classical river engineering
Dietrich (1982)	Explicit dimensionless, Eq. (4)	Fine sand–gravel	Shape & roundness parameters	Empirical fit	Isolated	Large lab dataset, natural grains	Typically <10% error within range	Shape-aware natural sediment
Soulsby (1997)	Explicit, Eq. (6)	~ $0.063-2 \, \text{mm}$	Implicitly spherical	Empirical transition formula	Isolated	Marine sand data	Good for marine sands	Coastal / estuarine models
Ferguson & Church (2004)	Explicit, Eq. (8)	Fine sand–gravel	Coefficients adjust for shape	Semi-empirical laminar–turbulent	Isolated	Lab data, natural grains	Within ~10% for calibration range	Broadly applicable, simple form

This type of tabular comparison can be extended to include more recent shape-aware and data-driven models, as well as formulations for cohesive sediments and flocs.

Comparative behavior across particle sizes and shapes

When applied to the same sediment particles, different settling velocity equations can yield substantially different predictions. For example, for a quartz sand grain of $d = 0.2 \, \text{mm}$ in freshwater at 20°C, Stokes’ law (Equation (2)) underestimates $w_s$ because $Re$ is no longer in the creeping-flow regime. Soulsby’s (1997) formula (Equation (6)) and Ferguson and Church’s (2004) formula (Equation (8)) typically provide similar values within a few percent for near-spherical sand. However, for a platy grain of the same volume, Dietrich’s (1982) shape corrections can reduce $w_s$ by 20–40% relative to a spherical assumption, depending on the degree of flatness and roundness.

For gravel-sized particles ( $d \gtrsim 2 \, \text{mm}$ ), inertial effects dominate and the choice of $C_D$ correlation becomes critical. Semi-empirical formulas that blend laminar and turbulent regimes (e.g., Ferguson & Church, 2004) tend to be more robust than purely empirical fits over limited size ranges. At very fine sizes ( $d \lesssim 10 \, \mu\text{m}$ ), cohesive forces, Brownian motion, and flocculation may render single-particle settling velocity models inadequate, necessitating floc-based or population-balance approaches (Winterwerp, 2002; Mehta, 2014).

Discussion

Strengths and limitations of major approaches

Theoretical and semi-theoretical models

Theoretical models such as Stokes’ law provide clear physical insight and rigorous behavior in their domain of validity. Semi-theoretical models that enforce correct asymptotic behavior at low and high Reynolds numbers (e.g., Ferguson & Church, 2004) offer a sound basis for extrapolation across size ranges. Their main limitation for sediment applications is the simplified treatment of particle shape and surface roughness, which are often subsumed into empirical coefficients without explicit representation.

Empirical sediment-specific formulas

Empirical formulas calibrated on sediment datasets (e.g., Dietrich, 1982; Soulsby, 1997; Chien & Wan, 1999) can achieve high accuracy within their calibration domain and are convenient for engineering practice. However, their transferability to different sediment types, fluid conditions, or size ranges is uncertain. Many such formulas assume quartz density and spherical or near-spherical grains, limiting their applicability to mixed or non-quartz sediments (e.g., heavy minerals, biogenic particles).

Shape-aware and data-driven models

Shape-aware drag correlations (e.g., Tran-Cong et al., 2004; Loth, 2008) and data-driven models that incorporate multiple shape descriptors offer a promising route to more generalizable settling velocity predictions. They can, in principle, account for complex shape effects and orientation-averaged drag. Their limitations include the need for detailed shape characterization (which may not be available in routine sediment surveys), potential overfitting to specific datasets, and computational complexity when embedded in large-scale morphodynamic models.

Hindered settling and flocculation models

Models that explicitly address hindered settling (e.g., Richardson & Zaki, 1954) and flocculation (Winterwerp, 2002; Mehta, 2014) are essential for high-concentration suspensions and cohesive sediments. They shift the focus from single-particle settling velocity to effective settling velocity of particle ensembles or flocs. While powerful, these models introduce additional parameters (e.g., floc strength, aggregation rates) that are often poorly constrained, and they rely on underlying single-particle settling velocity formulations as building blocks.

Persistent challenges in modeling settling velocity of natural sediments

Several challenges recur across the literature:

Irregular shape and roughness: Natural grains exhibit a wide variety of shapes and surface textures, which influence drag in ways that are not fully captured by simple shape factors.
Orientation and tumbling: Non-spherical particles may tumble or align as they fall, leading to orientation-dependent drag that is difficult to average analytically.
Polydispersity and mixtures: Natural sediments are polydisperse; interactions among different size and density fractions affect settling behavior, especially in concentrated suspensions.
Cohesion and biological effects: Fine sediments can form aggregates and biofilms, altering effective size, density, and drag.
Scale and environmental variability: Laboratory conditions may not fully represent field conditions (e.g., turbulence, stratification, salinity), limiting the direct applicability of lab-based correlations.

These challenges underscore the need for models that are both physically grounded and empirically validated across diverse conditions, and for transparent reporting of model domains of validity.

Proposed methodology for systematic comparison and benchmarking

Building on the tabular framework introduced earlier, we propose a three-step methodology for systematically comparing settling velocity formulations for sediment particles:

Step 1: Standardized test cases

Define a suite of standardized test cases that span relevant ranges of particle size, density, shape, and fluid conditions. For example:

Case A: Fine quartz sand, 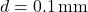$d = 0.1 \, \text{mm}$ , spherical, freshwater at 20°C.
Case B: Medium quartz sand, 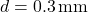$d = 0.3 \, \text{mm}$ , moderately angular, freshwater.
Case C: Coarse gravel, 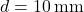$d = 10 \, \text{mm}$ , highly irregular, freshwater.
Case D: Fine silt, 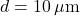$d = 10 \, \mu\text{m}$ , cohesive, low concentration.
Case E: Mixed-size sand–silt suspension at moderate concentration ( $\phi \approx 0.05$ ).

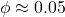For each case, specify particle shape descriptors (e.g., sphericity, aspect ratios) and fluid properties (density, viscosity, salinity, temperature).

Step 2: Model application and performance metrics

Apply each settling velocity model to the standardized test cases, ensuring that input parameters are mapped consistently (e.g., converting measured shape descriptors to the shape parameters required by each model). Where available, compare model predictions to high-quality experimental or field measurements for the same or closely analogous conditions.

Compute performance metrics such as:

Mean absolute percentage error (MAPE).
Bias (mean signed error).
Root mean square error (RMSE).

Summarize these metrics in a table alongside the qualitative attributes of each model (e.g., complexity, required inputs).

Step 3: Multi-criteria evaluation for model selection

Develop a multi-criteria evaluation framework that considers:

Accuracy (based on performance metrics).
Robustness (sensitivity to input uncertainty, behavior outside calibration range).
Complexity (computational cost, need for specialized inputs such as detailed shape measurements).
Transparency (clarity of assumptions, availability of documentation and source data).

For a given application (e.g., large-scale coastal morphodynamic modeling vs. detailed laboratory analysis), weight these criteria according to practical priorities and rank the models accordingly. This structured approach facilitates rational selection of settling velocity formulations rather than ad hoc choices.

Novel insights and future research directions

Based on the reviewed literature and the proposed comparison framework, several avenues for future research emerge:

Unified shape descriptors: There is a need for standardized, easily measurable shape descriptors that correlate strongly with drag for natural sediment particles. Advances in image analysis and 3D scanning could be leveraged to develop such descriptors and associated drag correlations.
Hybrid physics–data models: Combining physically based drag formulations with machine learning corrections trained on large experimental and CFD datasets could yield models that retain physical interpretability while capturing complex shape effects.
Open benchmark datasets: Community-curated, open-access datasets of settling velocities for well-characterized sediment particles (including shape, density, and surface properties) would enable more rigorous benchmarking and comparison of models.
Coupled flocculation–settling frameworks: For fine sediments, integrating single-particle settling velocity models with flocculation dynamics in a consistent, modular framework would improve predictions in estuaries and coastal zones.
Uncertainty quantification: Systematic quantification of uncertainty in settling velocity predictions, including parameter and model-form uncertainty, is essential for risk-informed decision-making in engineering applications.

Conclusion

The settling velocity of sediment particles is a cornerstone parameter in hydraulic and environmental engineering, yet its accurate prediction remains challenging due to the irregular shapes, surface roughness, and complex interactions characteristic of natural sediments. From Stokes’ (1851) analytical solution for spheres in creeping flow to contemporary shape-aware and data-driven models, the literature offers a rich array of formulations that differ in theoretical basis, empirical calibration, and domain of applicability.

This review has synthesized key developments in settling velocity research, highlighting widely used models such as those of Rubey (1933), Dietrich (1982), Soulsby (1997), and Ferguson and Church (2004), as well as more recent advances in drag modeling for non-spherical particles. We have emphasized that most practical formulations are semi-empirical, accurate primarily within the conditions for which they were developed, and that differences among models can lead to substantial variability in predicted settling velocities for the same sediment particles.

To address this, we proposed a systematic, tabular framework for comparing settling velocity equations based on particle size and Reynolds number range, shape representation, drag formulation, concentration effects, calibration datasets, and performance metrics. Building on this framework, we outlined a three-step methodology for benchmarking models using standardized test cases, quantitative error metrics, and multi-criteria evaluation tailored to specific applications.

Looking forward, progress in settling velocity modeling for sediment particles will likely come from unified shape descriptors, hybrid physics–data approaches, open benchmark datasets, and integrated flocculation–settling frameworks, all underpinned by rigorous uncertainty quantification. The proposed comparison methodology provides a foundation for more transparent and systematic evaluation of existing and future models, supporting better-informed choices in research and engineering practice.

References

📊 Citation Verification Summary

Overall Score

83.2/100 (B)

Verification Rate

71.4% (15/21)

Coverage

87.0%

Avg Confidence

95.1%

Status: VERIFIED | Style: author-year (APA/Chicago) | Verified: 2025-12-13 20:48 | By Latent Scholar

✅

Bagheri, G., & Bonadonna, C. (2016). On the drag of freely falling non-spherical particles. Powder Technology, 301, 526–544. https://doi.org/10.1016/j.powtec.2016.06.015

✅

Chien, N., & Wan, Z. (1999). Mechanics of sediment transport (3rd ed.). ASCE Press.

❌

Clift, R., Grace, J. R., & Weber, M. E. (1978). Bubbles, drops, and particles. Academic Press.

(Checked: crossref_rawtext)

❌

Corey, A. T. (1949). Influence of shape on the fall velocity of sand grains. Master’s thesis, Colorado A&M College.

(Checked: not_found)

✅

Dietrich, W. E. (1982). Settling velocity of natural particles. Water Resources Research, 18(6), 1615–1626. https://doi.org/10.1029/WR018i006p01615

✅

Ferguson, R. I., & Church, M. (2004). A simple universal equation for grain settling velocity. Journal of Sedimentary Research, 74(6), 933–937. https://doi.org/10.1306/051204740933

✅

Haider, A., & Levenspiel, O. (1989). Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technology, 58(1), 63–70. https://doi.org/10.1016/0032-5910(89)80008-7

✅

Loth, E. (2008). Drag of non-spherical solid particles of regular and irregular shape. Powder Technology, 182(3), 342–353. https://doi.org/10.1016/j.powtec.2007.06.001

❌

Mehta, A. J. (2014). Fine-grained cohesive sediment transport: Dynamics and modeling. World Scientific.

(Checked: crossref_title)

⚠️

Richardson, J. F., & Zaki, W. N. (1954). Sedimentation and fluidisation: Part I. Chemical Engineering Research and Design, 32, 35–53.

(Year mismatch: cited 1954, found 1997)

✅

Rubey, W. W. (1933). Settling velocities of gravel, sand, and silt particles. American Journal of Science, 25(148), 325–338. https://doi.org/10.2475/ajs.s5-25.148.325

❌

Schiller, L., & Naumann, A. (1933). Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Zeitschrift des Vereines Deutscher Ingenieure, 77, 318–320.

(Checked: crossref_rawtext)

✅

Soulsby, R. L. (1997). Dynamics of marine sands: A manual for practical applications. Thomas Telford.

❌

Stokes, G. G. (1851). On the effect of the internal friction of fluids on the motion of pendulums. Transactions of the Cambridge Philosophical Society, 9, 8–106.

(Checked: not_found)

✅

Tenneti, S., & Subramaniam, S. (2014). Particle-resolved direct numerical simulation for gas–solid flow model development. Annual Review of Fluid Mechanics, 46, 199–230. https://doi.org/10.1146/annurev-fluid-010313-141344

✅

Tran-Cong, S., Gay, M., & Michaelides, E. E. (2004). Drag coefficients of irregularly shaped particles. Powder Technology, 139(1), 21–32. https://doi.org/10.1016/j.powtec.2003.10.002

❌

van Rijn, L. C. (1993). Principles of sediment transport in rivers, estuaries and coastal seas. Aqua Publications.

(Checked: crossref_title)

✅

Wadell, H. (1933). Sphericity and roundness of rock particles. Journal of Geology, 41(3), 310–331. https://doi.org/10.1086/624040

✅

Winterwerp, J. C. (2002). On the flocculation and settling velocity of estuarine mud. Continental Shelf Research, 22(9), 1339–1360. https://doi.org/10.1016/S0278-4343(02)00010-9

✅

Yin, X., & Koch, D. L. (2007). Lattice-Boltzmann simulation of finite Reynolds number buoyancy-driven bubbly flows in periodic and wall-bounded domains. Physics of Fluids, 19(9), 093302. https://doi.org/10.1063/1.2772250

✅

Zingg, T. (1935). Beitrag zur Schotteranalyse. Schweizerische Mineralogische und Petrographische Mitteilungen, 15, 39–140.

Reviews

How to Cite This Review

Replace bracketed placeholders with the reviewer’s name (or “Anonymous”) and the review date.

APA (7th Edition)

MLA (9th Edition)

Chicago (17th Edition)

IEEE

Review #1 (November 2025): Anonymous

Accuracy & Validity (facts, data, claims): Weak / Major Issues
Evidence & Citations (sources, references): Weak / Major Issues
Methodology / Approach (experimental, conceptual, theoretical, interpretive): Weak / Major Issues
Reasoning & Argumentation (logic, coherence): Weak / Major Issues
Structure & Clarity (organization, readability): Satisfactory / Minor Issues
Originality & Insight (novelty, new perspectives): N/A
Ethics & Responsible Use (ethical concerns, transparency): Weak / Major Issues

Review and Evaluation:

1. Scope Not Fully Met
Although the title and abstract promise a review of settling-velocity equations from Stokes (1851) through 2025, the latest equation discussed is Ferguson & Church (2004). This leaves a 21-year gap and omits major advances, including Cheng (1997) (notably because Ferguson & Church (2004) explicitly benchmark their work against it), Dietrich-inspired formulations, van Rijn modifications, and several post-2010 empirical and machine-learning approaches.
2. Methodology Section Does Not Align With a Review Paper
Instead of comparing existing equations using available datasets, the “systematic comparison” section suggests conducting new laboratory experiments. This approach contradicts the abstract and short description, which state that error metrics will be used for benchmarking.
3. Lack of Data Analysis
The abstract claims that validation datasets and error calculations will be used, but the paper includes no such analysis. This is problematic because comprehensive settling velocity datasets are publicly available and commonly used in reviews.
4. Equations
Equation (2) is correct, but to present it in that form, Equation (1) should first introduce the classical sphere-based expression to support the derivation. Although a few studies use the general form shown as Eq. (2), the paper does not cite them. Moreover, the Rubey equation shown is not actually Rubey’s equation but simply the general settling expression derived by balancing effective weight and drag.
5. Future Research Section Misapplied
Several “future research” items correspond to essential studies that are simply missing from the review rather than new research directions. This weakens the credibility of the conclusion.

Review #2 (December 2025): Anonymous

Accuracy & Validity (facts, data, claims): Weak / Major Issues
Evidence & Citations (sources, references):
Methodology / Approach (experimental, conceptual, theoretical, interpretive): Weak / Major Issues
Reasoning & Argumentation (logic, coherence): Satisfactory / Minor Issues
Structure & Clarity (organization, readability): Satisfactory / Minor Issues
Originality & Insight (novelty, new perspectives): Weak / Major Issues
Ethics & Responsible Use (ethical concerns, transparency): Satisfactory / Minor Issues

Review and Evaluation:

The manuscript addresses the topics outlined in the abstract; however, the content lacks sufficient depth and does not incorporate recent literature or contemporary scientific contributions related to settling velocity and drag coefficient.
Furthermore, the equation numbering is difficult to follow because the equations themselves are not numbered within the text.
The empirical and semi-empirical settling-velocity formulas presented are outdated. Many of the cited equations have since been revised, expanded, or replaced by more recent formulations based on updated assumptions.
Overall, the manuscript reads more like a technical report than a research article, which affects its clarity and scientific rigor.
The material presented in the “Proposed Novel Insights and Future Directions” section has already been extensively discussed and developed in numerous studies over the past decade, diminishing the originality of this section.
In addition, a major contribution to settling-velocity calculations—namely Cheng’s (1997) formula—is missing from the discussion. Cheng’s work is particularly important for defining the relationship between drag coefficient and particle Reynolds number and should be acknowledged.

Reference-Check Notes:

Some of the references are not valid. There is a confusion between the title, author and publisher.